
分析 由题意可判断函数f(x)是R上的偶函数,且可判断在[0,+∞)上是增函数;从而可得x-1=x2-2x+1或x-1=-(x2-2x+1),从而解得.
解答 解:∵f(x)=x($\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$),
∴f(-x)=(-x)($\frac{1}{2}$-$\frac{1}{{2}^{-x}+1}$)
=x($\frac{1}{{2}^{-x}+1}$-$\frac{1}{2}$)=x($\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$)=f(x),
∴函数f(x)=x($\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$)是R上的偶函数,
∵f′(x)=($\frac{1}{2}$-$\frac{1}{{2}^{x}+1}$)+$\frac{x•{2}^{x}•ln2}{({2}^{x}+1)^{2}}$,
∴当x≥0时,f′(x)≥0;
故函数f(x)在[0,+∞)上是增函数;
∵f(x-1)=f(x2-2x+1),
∴x-1=x2-2x+1或x-1=-(x2-2x+1),
故x=1或x=2或x=0,
故答案为:3.
点评 本题考查了导数的综合应用及函数的性质的判断与应用.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
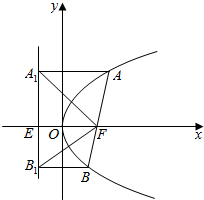 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com