
【题目】已知圆![]() ,直线
,直线![]() 过定点
过定点![]()
(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程。
的方程。
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程。
的方程。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() ,符合题意;若直线
,符合题意;若直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,由题意知,圆心
,由题意知,圆心![]() 到已知直线
到已知直线![]() 的距离等于半径
的距离等于半径![]() ,由此利用点到直线的距离公式得
,由此利用点到直线的距离公式得![]() ,从而求出直线的方程;(2)设直线方程为
,从而求出直线的方程;(2)设直线方程为![]() ,由弦长
,由弦长![]() 求出弦心距
求出弦心距![]() ,由此利用点到直线距离公式求出
,由此利用点到直线距离公式求出![]() 或
或![]() ,从而能求出直线
,从而能求出直线![]() 的方程.
的方程.
试题解析:(1)圆![]() 的圆心
的圆心![]() ,半径为2,
,半径为2,
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 为
为![]() ,显然满足条件,
,显然满足条件,
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() 即
即![]()
圆心到![]() 的距离
的距离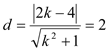 ,所以
,所以![]() ,
,![]() 的方程为
的方程为![]()
综上得所求![]() 的方程为
的方程为![]() 或
或![]() .
.
(2)由题意得圆心到![]() 的距离为
的距离为![]()
由(1)知当直线![]() 的斜率不存在时,不满足题意
的斜率不存在时,不满足题意
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() 即
即![]()
圆心到![]() 的距离
的距离![]() ,所以
,所以![]() ,
,
![]() 的方程为
的方程为![]() 或
或![]()


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是某企业2010年至2016年污水净化量(单位: 吨)的折线图.
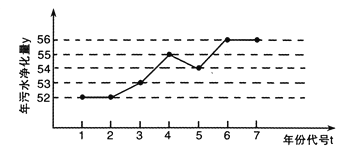
注: 年份代码1-7分别对应年份2010-2016.
(1)由折线图看出,可用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年该企业污水净化量;
年该企业污水净化量;
(3)请用数据说明回归方程预报的效果.
附注: 参考数据:![]() ;
;
参考公式:相关系数 ,回归方程
,回归方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分别为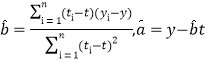 ;
;
反映回归效果的公式为: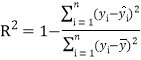 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回归的效果越好.
,表示回归的效果越好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 为常数,
为常数,![]() ).(Ⅰ)求函数
).(Ⅰ)求函数![]() 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当![]() 时,是否存在实数
时,是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范围;如果不存在,请说明理由(其中
的取值范围;如果不存在,请说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .现提供
.现提供![]() 的大致图像的8个选项:
的大致图像的8个选项:
(A)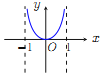 (B)
(B)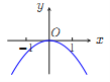 (C)
(C) (D)
(D)
(E) (F)
(F)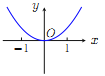 (G)
(G)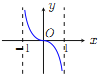 (H)
(H)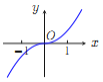
(Ⅰ)请你作出选择,你选的是( );
(Ⅱ)对于函数图像的判断,往往只需了解函数的基本性质.为了验证你的选择的正确性,请你解决下列问题:
①![]() 的定义域是 ;
的定义域是 ;
②就奇偶性而言, ![]() 是 ;
是 ;
③当![]() 时,
时, ![]() 的符号为正还是负?并证明你的结论.
的符号为正还是负?并证明你的结论.
(解决了上述三个问题,你要调整你的选项,还来得及.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O![]() 的直径,FB是圆台的一条母线.
的直径,FB是圆台的一条母线.
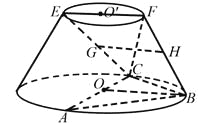
(Ⅰ)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=
AC=![]() ,AB=BC.求二面角
,AB=BC.求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com