
【题目】设![]() 为正整数,若两个项数都不小于
为正整数,若两个项数都不小于![]() 的数列
的数列![]() ,
,![]() 满足:存在正数
满足:存在正数![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() ,则称数列
,则称数列![]() ,
,![]() 是“
是“![]() 接近的”.已知无穷等比数列
接近的”.已知无穷等比数列![]() 满足
满足![]() ,无穷数列
,无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 通项公式;
通项公式;
(2)求证:对任意正整数![]() ,数列
,数列![]() ,
,![]() 是“
是“![]() 接近的”;
接近的”;
(3)给定正整数![]() ,数列
,数列![]() ,
,![]() (其中
(其中![]() )是“
)是“![]() 接近的”,求
接近的”,求![]() 的最小值,并求出此时的
的最小值,并求出此时的![]() (均用
(均用![]() 表示).(参考数据:
表示).(参考数据:![]() )
)
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]() 的最小值
的最小值![]() ,此时
,此时![]()
【解析】
(1)设等比数列![]() 公比为
公比为![]() ,由
,由![]() ,可求得首项和公比,进而求得通项;
,可求得首项和公比,进而求得通项;
(2)只需证明![]() 成立,即可得证;
成立,即可得证;
(3)由题设可求得![]() ,根据定义进而得到
,根据定义进而得到![]() 对
对![]() 都成立,再构造函数求解即可.
都成立,再构造函数求解即可.
(1)设等比数列![]() 公比为
公比为![]() ,由
,由![]() 得
得![]() ,解得
,解得![]() ,故
,故![]() .
.
(2)![]()
 .
.
对任意正整数![]() ,当
,当![]() ,且
,且![]() 时,有
时,有![]() ,
,
则![]() ,即
,即![]() 成立,
成立,
故对任意正整数![]() ,数列
,数列![]() ,
,![]() 是“
是“![]() 接近的”.
接近的”.
(3)由![]() ,得到
,得到![]() ,且
,且![]() ,
,
从而![]() ,于是
,于是![]() .
.
当![]() 时,
时,![]() ,
,![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,又
,又![]() ,
,
整理得![]() ,所以
,所以![]() ,因此数列
,因此数列![]() 为等差数列.
为等差数列.
又因为![]() ,
,![]() ,则数列
,则数列![]() 的公差为1,故
的公差为1,故![]() .
.
根据条件,对于给定正整数![]() ,当
,当![]() 且
且![]() 时,都有
时,都有
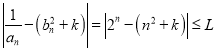 成立,
成立,
即![]() ①对
①对![]() 都成立.
都成立.
考察函数![]() ,
,![]() ,令
,令![]() ,
,
则![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上是增函数.
上是增函数.
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上是增函数.
上是增函数.
注意到![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
![]() 的最小值为
的最小值为![]() .
.
欲使满足①的实数![]() 存在,必有
存在,必有![]() ,即
,即![]() ,
,
因此![]() 的最小值
的最小值![]() ,此时
,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】如图是某商场2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图(例如:第3季度内,洗衣机销量约占![]() ,电视机销量约占
,电视机销量约占![]() ,电冰箱销量约占
,电冰箱销量约占![]() ).根据该图,以下结论中一定正确的是( )
).根据该图,以下结论中一定正确的是( )
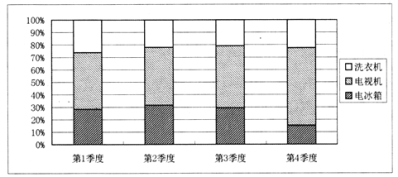
A. 电视机销量最大的是第4季度
B. 电冰箱销量最小的是第4季度
C. 电视机的全年销量最大
D. 电冰箱的全年销量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点.
上的动点.
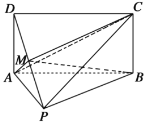
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积记为
的体积记为![]() ,四棱锥
,四棱锥![]() 的体积记为
的体积记为![]() ,当
,当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() .如果数列
.如果数列![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() ,则称
,则称![]() 为
为![]() 的“衍生数列”.
的“衍生数列”.
(Ⅰ)若数列![]() 的“衍生数列”是
的“衍生数列”是![]() ,求
,求![]() ;
;
(Ⅱ)若![]() 为偶数,且
为偶数,且![]() 的“衍生数列”是
的“衍生数列”是![]() ,证明:
,证明:![]() 的“衍生数列”是
的“衍生数列”是![]() ;
;
(Ⅲ)若![]() 为奇数,且
为奇数,且![]() 的“衍生数列”是
的“衍生数列”是![]() ,
,![]() 的“衍生数列”是
的“衍生数列”是![]() ,….依次将数列
,….依次将数列![]() ,
,![]() ,
,![]() ,…的第
,…的第![]() 项取出,构成数列
项取出,构成数列![]() .证明:
.证明:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 数列
数列![]() 满足
满足![]() ;数列
;数列![]() 满足
满足![]() ;数列
;数列![]() 为公比大于1的等比数列,且
为公比大于1的等比数列,且![]() ,
,![]() 为方程
为方程![]() 的两个不相等的实根.
的两个不相等的实根.
(1)求数列![]() 和数列
和数列![]() 的通项公式;
的通项公式;
(2)将数列![]() 中的第
中的第![]() 项,第
项,第![]() 项,第
项,第![]() 项,……,第
项,……,第![]() 项,……删去后剩余的项按从小到大的顺序排成新数列
项,……删去后剩余的项按从小到大的顺序排成新数列![]() ,求数列
,求数列![]() 的前2013项和.
的前2013项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]()
![]() 都在双曲线
都在双曲线![]() 上,直线
上,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,设坐标原点为
,设坐标原点为![]() .
.
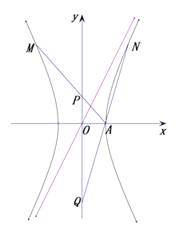
(1)求双曲线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .问:在
.问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,试求直线
,试求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com