
【题目】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.
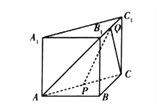
(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
科目:高中数学 来源: 题型:
【题目】函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x).当x∈[0,1]时,f(x)=2x.若在区间[﹣2,3]上方程ax+2a﹣f(x)=0恰有四个不相等的实数根,则实数a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,2)
,2)
D.(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,点M(x0 , 2 ![]() )(x0>
)(x0> ![]() )是抛物线C上一点,圆M与线段MF相交于点A,且被直线x=
)是抛物线C上一点,圆M与线段MF相交于点A,且被直线x= ![]() 截得的弦长为
截得的弦长为 ![]() |MA|,若
|MA|,若 ![]() =2,则|AF|等于( )
=2,则|AF|等于( )
A.![]()
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为( )
A.(﹣∞,e]
B.[0,e]
C.(﹣∞,e)
D.[0,e)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有命题:
①y=|sinx-![]() |的周期是2π;
|的周期是2π;
②y=sinx+sin|x|的值域是[0,2] ;
③方程cosx=lgx有三解;
④![]() 为正实数,
为正实数,![]() 在
在![]() 上递增,那么
上递增,那么![]() 的取值范围是
的取值范围是![]() ;
;
⑤在y=3sin(2x+![]() )中,若f(x
)中,若f(x![]() )=f(x2)=0,则x1-x2必为
)=f(x2)=0,则x1-x2必为![]() 的整数倍;
的整数倍;
⑥若A、B是锐角△ABC的两个内角,则点P(cosB-sinA,sinB-cosA)在第二象限;
⑦在![]() 中,若
中,若![]() ,则
,则![]() 钝角三角形。
钝角三角形。
其中真命题个数为( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M: ![]() 和点
和点 ![]() ,动圆P经过点N且与圆M相切,圆心P的轨迹为曲线E.
,动圆P经过点N且与圆M相切,圆心P的轨迹为曲线E.
(1)求曲线E的方程;
(2)点A是曲线E与x轴正半轴的交点,点B,C在曲线E上,若直线AB,AC的斜率分别是k1 , k2 , 满足k1k2=9,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ②若
②若![]() ,则
,则![]()
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]()
其中正确命题的序号是( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com