
袋中装有大小和形状相同的小球若干个黑球和白球,且黑球和白球的个数比为4:3,从中任取2个球都是白球的概率为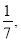 现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.
(1)求袋中原有白球、黑球的个数;
(2)求随机变量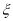 的分布列和数学期望.
的分布列和数学期望.
(1)袋中原有3个白球和4个黑球;(2)分布列详见解析, .
.
【解析】
试题分析:本题主要考查古典概型、离散型随机变量的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,设出袋中白球和黑球个数,由于从中任取2个都是白球,则可列出 ,利用组合数的计算,计算出n的值,从而得到白球和黑球个数;第二问,利用第一问的结论,利用不放回抽样,计算出每一种情况的概率,列出分布列,利用
,利用组合数的计算,计算出n的值,从而得到白球和黑球个数;第二问,利用第一问的结论,利用不放回抽样,计算出每一种情况的概率,列出分布列,利用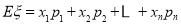 计算出数学期望.
计算出数学期望.
(1)依题意设袋中原有 个白球,则有
个白球,则有 个黑球.
个黑球.
由题意知 , 4分
, 4分
即 ,解得
,解得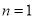 ,
,
即袋中原有3个白球和4个黑球. 5分
(2)依题意, 的取值是
的取值是 .
.
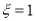 ,即第1次取到白球,
,即第1次取到白球,
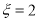 ,即第2次取到白球
,即第2次取到白球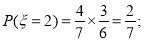
同理可得,

 10分
10分
 分布列为
分布列为
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
 12分
12分
考点:古典概型、离散型随机变量的分布列和数学期望.


科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
各项均为正数的数列{an}中,设 ,
, ,且
,且 ,
, .
.
(1)设 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设 ,求集合
,求集合 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:解答题
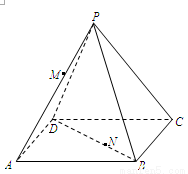
如图,在正四棱锥P-ABCD中,PA=AB= ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN= BD.
BD.
(1)若PM= PA,求证:MN⊥AD;
PA,求证:MN⊥AD;
(2)若二面角M-BD-A的大小为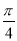 ,求线段MN的长度.
,求线段MN的长度.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
已知m,n是不重合的两条直线,α,β是不重合的两个平面.下列命题:
①若α⊥β,m⊥α,则m∥β; ②若m⊥α,m⊥β,则α∥β;
③若m∥α,m⊥n,则n⊥α; ④若m∥α,m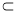 β,则α∥β.
β,则α∥β.
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
已知全集U=R,集合A={x|x≤-2,x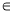 R},B={x|x<1,x
R},B={x|x<1,x R},则(∁UA)∩B= .
R},则(∁UA)∩B= .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输出的结果是 ,则判断框内的条件( )
,则判断框内的条件( )

A.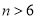 ? B.
? B. ? C.
? C. ? D.
? D. ?
?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省韶关市高三4月高考模拟(二模)文科数学试卷(解析版) 题型:选择题
给出如下四个判断:
①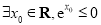 ;
;
②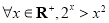 ;
;
③设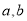 是实数,
是实数,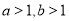 是
是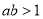 的充要条件 ;
的充要条件 ;
④命题“若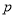 则
则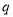 ”的逆否命题是若
”的逆否命题是若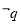 ,则
,则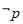 .
.
其中正确的判断个数是:
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省肇庆市高三3月第一次模拟文科数学试卷(解析版) 题型:选择题
设向量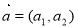 ,
,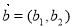 ,定义一种向量积:
,定义一种向量积: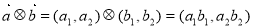 .已知向量
.已知向量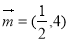 ,
,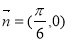 ,点P在
,点P在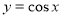 的图象上运动,点Q在
的图象上运动,点Q在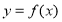 的图象上运动,且满足
的图象上运动,且满足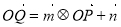 (其中O为坐标原点),则
(其中O为坐标原点),则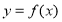 在区间
在区间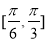 上的最大值是( )
上的最大值是( )
A.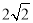 B.
B.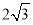 C.
C.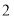 D.
D.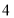
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com