
【题目】设![]() .
.
(1)求![]() 的反函数
的反函数![]() ;
;
(2)讨论![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(3)令![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上的值域是
上的值域是![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)令![]() ,由求反函数的规则解出
,由求反函数的规则解出![]() .
.
(2)复合函数,外层函数的单调性要由底数![]() 的取值范围确定,分两类讨论,内层函数的单调性可由定义法证明,再由复合函数的单调性判断出函数的单调性即可.
的取值范围确定,分两类讨论,内层函数的单调性可由定义法证明,再由复合函数的单调性判断出函数的单调性即可.
(3)分类讨论当![]() 时,和
时,和![]() 时两种情况,由(2)中单调性解出
时两种情况,由(2)中单调性解出![]() 的取值范围,并起来即可得到符合条件的参数的取值范围.
的取值范围,并起来即可得到符合条件的参数的取值范围.
(1)令![]() ,解得
,解得![]()
(2)令![]() ,设
,设![]()
![]() 在
在![]() 上单调递增.
上单调递增.
当![]() 时,根据复合函数单调性得到
时,根据复合函数单调性得到![]() 在
在![]() 上是减函数.
上是减函数.
当![]() 时,根据复合函数单调性得到
时,根据复合函数单调性得到![]() 在
在![]() 上是增函数.
上是增函数.
综上所述:当![]() 时,
时,![]() 在
在![]() 上是减函数;当
上是减函数;当![]() 时,
时, ![]() 在
在![]() 上是增函数.
上是增函数.
(3)当![]() 时,
时,![]() 在
在![]() 上是减函数,
上是减函数,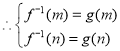
即有![]() 得
得![]() ,即
,即![]() ,
,
可知方程的两个根均大于1,故有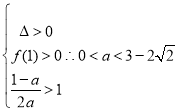
当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
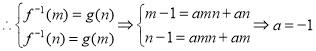 (舍去).
(舍去).
综上所述:![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左顶点为
,左顶点为![]() ,过点
,过点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() 为
为![]() 的中点,是否存在定点
的中点,是否存在定点![]() ,对于任意的
,对于任意的![]() 都有
都有![]() ,若存在,求出点
,若存在,求出点![]() 的
的
坐标;若不存在说明理由;
(3)若过![]() 点作直线
点作直线![]() 的平行线交椭圆
的平行线交椭圆![]() 于点
于点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个生产公司投资A生产线500万元,每万元可创造利润![]() 万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了
万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了![]() ;若将少用的x万元全部投入B生产线,每万元创造的利润为
;若将少用的x万元全部投入B生产线,每万元创造的利润为![]() 万元,其中
万元,其中![]() .
.
![]() 若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
![]() 若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次数学知识竞赛中,两组学生成绩如下表:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
已经算得两个组的平均分都是80分,请根据你所学过的统计知识,进一步判断这两个组这次竞赛中成绩谁优谁次,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的焦点是椭圆
的焦点是椭圆![]() 的顶点,
的顶点, ![]() 为椭圆
为椭圆![]() 的左焦点且椭圆
的左焦点且椭圆![]() 经过点
经过点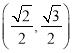 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右顶点
的右顶点![]() 作斜率为
作斜率为![]() 的直线交椭圆
的直线交椭圆![]() 于另一点
于另一点![]() ,连结
,连结![]() 并延长
并延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,当
,当![]() 的面积取得最大值时,求
的面积取得最大值时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运动会时,高一某班共有28名同学参加比赛,每人至多报两个项目.15人参加游泳,8人参加田径,14人参加球类.同时参加游泳和田径的有3人,同时参加游泳和球类的有3人,则只参加一个项目的有______人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以原点
),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,若点
上一点,若点![]() 到曲线
到曲线![]() 的最小距离为
的最小距离为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com