
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 经过原点的切线方程;
经过原点的切线方程;
(Ⅱ)若在![]() 时,有
时,有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】今年,楼市火爆,特别是一线城市.某一线城市采取“限价房”摇号制度,客户以家庭为单位进行抽签,若有![]() 套房源,则设置
套房源,则设置![]() 个中奖签,客户抽到中奖签视为中签,中签家庭可以在指定小区提供的房源中随机抽取一个房号,现共有20户家庭去抽取6套房源.
个中奖签,客户抽到中奖签视为中签,中签家庭可以在指定小区提供的房源中随机抽取一个房号,现共有20户家庭去抽取6套房源.
(l)求每个家庭能中签的概率;
(2)已知甲、乙两个友好家庭均已中签,并共同前往某指定小区抽取房号,目前该小区剩余房源有某单元27、28两个楼层共6套房,其中,第27层有2套房,第28层有4套房.记甲、乙两个家庭抽取到第28层的房源套数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
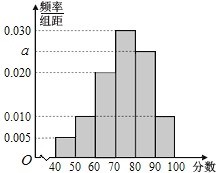
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为A的函数f(x),若对任意的x1,x2∈A,都有f(x1+x2)-f(x1)≤f(x2),则称函数f(x)为“定义域上的M函数”,给出以下五个函数:
①f(x)=2x+3,x∈R;②f(x)=x2,x∈![]() ;③f(x)=x2+1,x∈
;③f(x)=x2+1,x∈![]() ;④f(x)=sin x,x∈
;④f(x)=sin x,x∈![]() ;⑤f(x)=log2x,x∈[2,+∞).
;⑤f(x)=log2x,x∈[2,+∞).
其中是“定义域上的M函数”的有( )
A. 2个 B. 3个
C. 4个 D. 5个
查看答案和解析>>
科目:高中数学 来源: 题型:
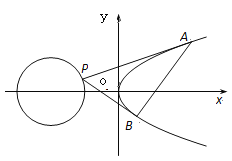
【题目】设点![]() 为抛物线
为抛物线![]() 外一点,过点
外一点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.
(Ⅰ)若点![]() 为
为![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若点![]() 为圆
为圆![]() 上的点,记两切线
上的点,记两切线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足;对任意
,如果满足;对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.已知函数
的上界.已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的值域,并判断函数
上的值域,并判断函数![]() 在
在![]() 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(Ⅱ)若![]() 是
是![]() 上的有界函数,且
上的有界函数,且![]() 的上界为3,求实数
的上界为3,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求函数
,求函数![]() 在
在![]() 上的上界
上的上界![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com