
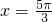 对称,求函数y=bsinx+acosx的对称轴.
对称,求函数y=bsinx+acosx的对称轴.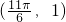 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得y=f(x)的图象,又知f(x)=3的所有正根从小到大依次为x1,x2,x3,…,xn,…,且xn-xn-1=3(n≥2),求f(x)的解析式.
倍,然后向左平移1个单位可得y=f(x)的图象,又知f(x)=3的所有正根从小到大依次为x1,x2,x3,…,xn,…,且xn-xn-1=3(n≥2),求f(x)的解析式. 对称,
对称,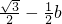 |=
|=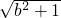 ,∴b=-
,∴b=- .
. sinx+cosx=
sinx+cosx= cos(x+
cos(x+ ).
). =kπ,k∈z,可得函数的对称轴为:x=kπ-
=kπ,k∈z,可得函数的对称轴为:x=kπ- ,k∈z.
,k∈z.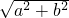 sin(x+∅)+c,其中,sin∅=
sin(x+∅)+c,其中,sin∅= ,cos∅=
,cos∅= .
. ,1),所以
,1),所以 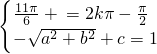 ,
, ,
, )+c.
)+c. 倍,然后向左平移1个单位可得y=f(x)的图象,则f(x)=(c-1)sin
倍,然后向左平移1个单位可得y=f(x)的图象,则f(x)=(c-1)sin x+c.
x+c.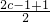 ,
,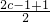 =3,解得c=2 或 c=3.
=3,解得c=2 或 c=3.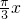 +2,T=6.
+2,T=6.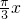 +2相交,且 xn-xn-1=3 (n≥2 ),周期为3(矛盾).
+2相交,且 xn-xn-1=3 (n≥2 ),周期为3(矛盾).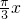 +3,T=6.
+3,T=6. 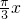 +3相交,且 xn-xn-1=3 (n≥2 ),周期为6(满足条件).
+3相交,且 xn-xn-1=3 (n≥2 ),周期为6(满足条件).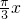 +2.
+2. 对称,求出b的值,可得函数 y=
对称,求出b的值,可得函数 y= cos(x+
cos(x+ ),由 x+
),由 x+ =kπ,k∈z,求出x的解析式,即可得到函数的对称轴方程.
=kπ,k∈z,求出x的解析式,即可得到函数的对称轴方程. ,1),求得g(x)=(c-1)sin(x-
,1),求得g(x)=(c-1)sin(x- )+c.再由函数图象的变换规律求得f(x)=(c-1)sin
)+c.再由函数图象的变换规律求得f(x)=(c-1)sin x+c.由题意可得,直线y=3要么过f(x)的最高点或最低点,或过f(x)的对称中心.分别求出c的值,再检验得出结论.
x+c.由题意可得,直线y=3要么过f(x)的最高点或最低点,或过f(x)的对称中心.分别求出c的值,再检验得出结论.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| a+lnx |
| x |
| (x+1)lnx |
| x |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| lnx |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com