练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】[选修4-4：坐标系与参数方程]
    已知在直角坐标系xOy中，曲线C的参数方程为 （φ为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，直线l的方程为ρcos（θ﹣ ）=2 ．
    （Ⅰ）求曲线C在极坐标系中的方程；
    （Ⅱ）求直线l被曲线C截得的弦长．

    【答案】解：（Ⅰ）曲线C的参数方程为 （φ为参数），普通方程为x2+（y﹣2）2=4，即x2+y2﹣4y=0， ∴曲线C在极坐标系中的方程为ρ=4sinθ；
    （Ⅱ）直线l的方程为ρcos（θ﹣ ）=2 ，即x+y﹣4=0，
    圆心到直线的距离d= = ，
    ∴直线l被曲线C截得的弦长=2 =2 ．
    【解析】（Ⅰ）求出曲线C的普通方程，即可求曲线C在极坐标系中的方程；（Ⅱ）求出圆心到直线的距离，利用勾股定理求直线l被曲线C截得的弦长．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体ABCDEF中，四边形ABCD为边长为4的正方形，M是BC的中点，EF∥平面ABCD，且EF=2，AE=DE=BF=CF= ．
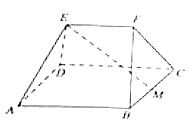
    （1）求证：ME⊥平面ADE；
    （2）求二面角B﹣AE﹣D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣ ﹣2lnx，a∈R．
    （1）讨论函数f（x）的单调性；
    （2）若函数f（x）有两个极值点x1 ， x2 ， 且x1＜x2 ， 求a的取值范围；
    （3）在（2）的条件下，证明：f（x2）＜x2﹣1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》第三章“衰分”介绍比例分配问题：“衰分”是按比例递减分配的意思，通常称递减的比例（百分比）为“衰分比”．如：甲、乙、丙、丁衰分得100，60，36，21.6个单位，递减的比例为40%，今共有粮m（m＞0）石，按甲、乙、丙、丁的顺序进行“衰分”，已知丙衰分得80石，乙、丁衰分所得的和为164石，则“衰分比”与m的值分别为（ ）
    A.20% 369
    B.80% 369
    C.40% 360
    D.60% 365

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，三角形ABC和梯形ACEF所在的平面互相垂直，AB⊥BC，AF⊥AC，AF 2CE，G是线段BF上一点，AB=AF=BC．
    （Ⅰ）若EG∥平面ABC，求 的值；
    （Ⅱ）求二面角A﹣BF﹣E的大小的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x1，x2∈.

    求证：tan x1＋tan x2＞2tan.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，点O为数轴的原点，A，B，M为数轴上三点，C为线段OM上的动点．设x表示点C与原点的距离，y表示点C到点A的距离的4倍与点C到点B的距离的6倍之和．

    (1)将y表示为x的函数；

    (2)要使y的值不超过70，实数x应该在什么范围内取值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线和椭圆有公共的焦点，且离心率为．

    （Ⅰ）求双曲线的方程．

    （Ⅱ）经过点作直线交双曲线于， 两点，且为的中点，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在正方形ABCD中，点E，F分别是AB，BC的中点，BD与EF交于点H，G为BD中点，点R在线段BH上，且 =λ（λ＞0）．现将△AED，△CFD，△DEF分别沿DE，DF，EF折起，使点A，C重合于点B（该点记为P），如图2所示．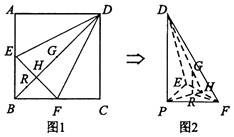

    （I）若λ=2，求证：GR⊥平面PEF；
    （Ⅱ）是否存在正实数λ，使得直线FR与平面DEF所成角的正弦值为 ？若存在，求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案