
分析 画出函数f(x)=$\left\{\begin{array}{l}{{2}^{x},}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$的图象;
(1)根据函数f(x)的图象与x轴无交点,得到f(x)无零点;
(2)若g(x)=0有且只有一个根,则-k∈(0,1),进而得到k的范围;
(3)当k=-1时,g(x)的图象与x轴有两个交点,(-1,0)和(0,0),进而得到零点;
(4)若方程g(x)=0总有两个根,则-k∈[1,+∞),进而得到k的范围;
解答 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{x},}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$的图象如下图所示: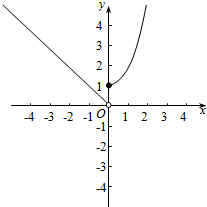
(1)由图可得:函数f(x)=$\left\{\begin{array}{l}{{2}^{x},}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$的图象与x轴无交点,
故f(x)无零点;
(2)∵g(x)=f(x)+k,若g(x)=0,则f(x)=-k,
若方程g(x)=0有其只有一个根,
则-k∈(0,1),
即k∈(-1,0),
(3)当k=-1时,g(x)=f(x)-1,其图象与x轴有两个交点,(-1,0)和(0,0),
故g(x)有两个零点,分别为-1和0;
(4)若方程g(x)=0总有两个根,
则-k∈[1,+∞),
即k∈(-∞,-1].
点评 本题考查的知识点是函数的零点,数形结合是解答此类问题常用的办法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com