
【题目】如图,在三棱柱![]() 中,
中, ![]() ,
, ![]() 是线段
是线段![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
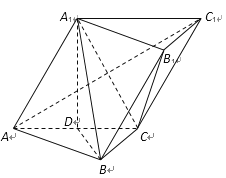
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() 平面
平面![]() ;
;
(Ⅲ)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)![]()
【解析】试题分析:(Ⅰ)由![]() ,可得
,可得![]() ,由
,由![]() 平面
平面![]() 可得
可得![]() .根据线面垂直的判定定理可得
.根据线面垂直的判定定理可得![]() 平面
平面![]() ,再利用面面垂直的判定定理可得结论;(Ⅱ)连接
,再利用面面垂直的判定定理可得结论;(Ⅱ)连接![]() ,设
,设![]() ,根据三角形中位线定理可得
,根据三角形中位线定理可得![]() ,从而根据线面平行的判定定理可得
,从而根据线面平行的判定定理可得![]() 平面
平面![]() ;(Ⅲ)取
;(Ⅲ)取![]() 的中点
的中点![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,又因为
,又因为![]() 平面
平面![]() ,所以
,所以![]() 两两垂直.以
两两垂直.以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴建立空间坐标系,利用向量垂直数量积为零列方程组,分别求出平面
轴建立空间坐标系,利用向量垂直数量积为零列方程组,分别求出平面![]() 的一个法向量与平面
的一个法向量与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(Ⅰ)证明:因为![]() ,所以
,所以![]() .
.
根据题意, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
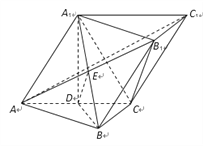
(Ⅱ)证明:连接![]() ,设
,设![]() ,连接
,连接![]() 根据棱柱的性质可知,
根据棱柱的性质可知, ![]() 为
为![]() 的中点,因为
的中点,因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .又因为
.又因为![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
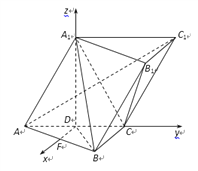
(Ⅲ)如图,取![]() 的中点
的中点![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 两两垂直.以
两两垂直.以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴建立空间坐标系(如图).
轴建立空间坐标系(如图).
由(Ⅰ)可知, ![]() 平面
平面![]() ,
,
所以![]() .又因为
.又因为![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,所以四边形
,所以四边形![]() 为菱形.
为菱形.
由已知![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
因为![]() ,
, ![]() ,所以
,所以![]() ,即
,即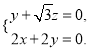
设![]() ,则
,则![]() .
.
再设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
因为![]() ,
, ![]() ,所以
,所以![]() ,即
,即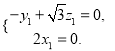
设![]() ,则
,则![]() .故
.故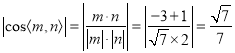 .
.
由图知,二面角![]() 的平面角为锐角,
的平面角为锐角,
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的证明以及利用空间向量求二面角,属于难题. 空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
![]()
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若花店一天购进17枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)若花店计划一天购进16枝或17枝玫瑰花,以利润角度看,你认为应购进16枝好还是17枝好?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N的距离的![]() 倍.
倍.
(1)求曲线E的方程;
(2)已知m≠0,设直线![]() :x﹣my﹣1=0交曲线E于A,C两点,直线
:x﹣my﹣1=0交曲线E于A,C两点,直线![]() :mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
:mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(1)求![]() ;
;
(2)除H以外,直线MH与C是否有其它公共点?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com