
【题目】在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4
(1)若直线l过点A(4,0),且被圆C1截得的弦长为2 ![]() ,求直线l的方程
,求直线l的方程
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2 , 它们分别与圆C1和C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,求所有满足条件的点P的坐标.
【答案】
(1)解:由于直线x=4与圆C1不相交;
∴直线l的斜率存在,设l方程为:y=k(x﹣4)
圆C1的圆心到直线l的距离为d,∵l被⊙C1截得的弦长为2 ![]()
∴d= ![]() =1
=1
d= ![]() 从而k(24k+7)=0即k=0或k=﹣
从而k(24k+7)=0即k=0或k=﹣ ![]()
∴直线l的方程为:y=0或7x+24y﹣28=0
(2)解:设点P(a,b)满足条件,
由题意分析可得直线l1、l2的斜率均存在且不为0,
不妨设直线l1的方程为y﹣b=k(x﹣a),k≠0
则直线l2方程为:y﹣b=﹣ ![]() (x﹣a)
(x﹣a)
∵⊙C1和⊙C2的半径相等,及直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,
∴⊙C1的圆心到直线l1的距离和圆C2的圆心到直线l2的距离相等
即 ![]() =
= 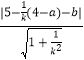
整理得|1+3k+ak﹣b|=|5k+4﹣a﹣bk|
∴1+3k+ak﹣b=±(5k+4﹣a﹣bk)即(a+b﹣2)k=b﹣a+3或(a﹣b+8)k=a+b﹣5
因k的取值有无穷多个,所以 ![]() 或
或 ![]()
解得 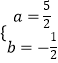 或
或 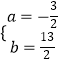
这样的点只可能是点P1( ![]() ,﹣
,﹣ ![]() )或点P2(﹣
)或点P2(﹣ ![]() ,
, ![]() )
)
【解析】(1)因为直线l过点A(4,0),故可以设出直线l的点斜式方程,又由直线被圆C1截得的弦长为2 ![]() ,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,即圆心到直线的距离,得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l的方程.(2)与(1)相同,我们可以设出过P点的直线l1与l2的点斜式方程,由于两直线斜率为1,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,故我们可以得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l1与l2的方程.
,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,即圆心到直线的距离,得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l的方程.(2)与(1)相同,我们可以设出过P点的直线l1与l2的点斜式方程,由于两直线斜率为1,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,故我们可以得到一个关于直线斜率k的方程,解方程求出k值,代入即得直线l1与l2的方程.
【考点精析】本题主要考查了一般式方程的相关知识点,需要掌握直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0)才能正确解答此题.
(A,B不同时为0)才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】四边形ABCD中, ![]() =(3,2),
=(3,2), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3)
=(﹣2,﹣3)
(1)若 ![]() ∥
∥ ![]() ,试求x与y满足的关系式;
,试求x与y满足的关系式;
(2)满足(1)同时又有 ![]() ⊥
⊥ ![]() ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)+f(2﹣x)=2,当x∈(0,1]时,f(x)=x2 , 当x∈(﹣1,0]时, ![]() ,若定义在(﹣1,3)上的函数g(x)=f(x)﹣t(x+1)有三个不同的零点,则实数t的取值范围是( )
,若定义在(﹣1,3)上的函数g(x)=f(x)﹣t(x+1)有三个不同的零点,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩数字游戏,先由甲任想一个数字记为a,再由乙猜甲刚才想的数字,把乙想的数字记为b,且a,b∈{1,2,3,4,5,6},记ξ=|a﹣b|.
(1)求ξ=1的概率;
(2)若ξ≤1,则称“甲乙心有灵犀”,求“甲乙心有灵犀”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一![]() 名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分
名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分![]() 分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.

(1)填写答题卡频率分布表中的空格, 补全频率分布直方图, 并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级的平均数及中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() 上任意一点,点
上任意一点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 分别与线段
分别与线段![]() 交于
交于![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设
两点,设![]() 为坐标原点,
为坐标原点, ![]() ,判断
,判断![]() 的面积是否为定值?若是,求出定值,若不是,说明理由.
的面积是否为定值?若是,求出定值,若不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com