
【题目】已知![]() 是定义在(0,+∞)上的增函数,且满足
是定义在(0,+∞)上的增函数,且满足![]() =
=![]() +
+![]() =1.
=1.
(1)求证: ![]() =3;
=3;
(2)求不等式![]() >3的解集.
>3的解集.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】某商品在最近100天内的价格f(t)与时间t的函数关系式是

销售量g(t)与时间t的函数关系式是g(t)=-![]() +
+![]() (0≤t≤100),求这种商品的日销售额的最大值.
(0≤t≤100),求这种商品的日销售额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱锥P﹣ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点. 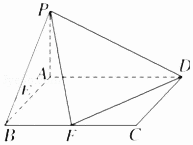
(1)证明:PF⊥FD;
(2)若PA=1,求点E到平面PFD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节7家超市的广告费支出x(万元)和销售额y(万元)数据如下,
超市 | A | B | C | D | E | F | G |
广告费支出x | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额y | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)请根据上表提供的数据.用最小二乘法求出y关于x的线性回归方程; ![]() =
= ![]() x+
x+ ![]()
(2)用二次函数回归模型拟合y与x的关系,可得回归方程: ![]() =﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
=﹣0.17x2+5x+20. 经计算二次函数回归模型和线性回归模型的R2分别约为0.93和0.75,请用R2说明选择哪个回归模型更合适.并用此模型预测A超市广告费支出为3万元时的销售额,
参考数据及公式: ![]() =8,
=8, ![]() =42.
=42. ![]() xiyi=2794,
xiyi=2794, ![]() x
x ![]() =708,
=708,![]() =
= 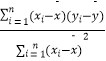 =
= 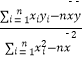 ,
, ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某纺织厂订购一批棉花,其各种长度的纤维所占的比例如下表所示:

(1)请估计这批棉花纤维的平均长度与方差.
(2)如果规定这批棉花纤维的平均长度为4.90厘米,方差不超过1.200,两者允许误差均不超过0.10视为合格产品.请你估计这批棉花的质量是否合格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数
,那么该函数![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)用函数单调性定义来证明![]() 上的单调性;
上的单调性;
(2)已知![]() ,
, ![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)对于(2)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com