
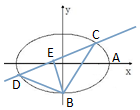
���� ��1������������$e=\frac{{\sqrt{2}}}{2}$��ԭ�㵽����A��a��0����B��0��-b����ֱ�ߵľ�����$\frac{{\sqrt{6}}}{3}$���г���������⼴�ɵõ���Բ�ķ��̣�
��2������$\left\{{\begin{array}{l}{\frac{x^2}{2}+{y^2}=1}\\{y=kx+m}\end{array}}\right.$��y��������C��x1��y1����D��x2��y2����CD���е���E��x0��y0��������Τ�ﶨ�����${x_0}=-\frac{km}{{\frac{1}{2}+{k^2}}}��{y_0}=k{x_0}+m$�����BE�ķ���x0+ky0+k=0�������Ƴ�m=1+2k2�����m�ʣ�0��1��˵��������������ֱ�ߣ�����Բ�ڲ�ͬ�����㣬�������㶼����BΪԲ�ĵ�Բ�ϣ�
���  ����С������12�֣�
����С������12�֣�
�⣺��1����$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$��c2=a2-b2����1�֣�
ԭ�㵽ֱ��AB��$\frac{x}{a}-\frac{y}{b}=1$�ľ���$d=\frac{ab}{{\sqrt{{a^2}+{b^2}}}}=\frac{{\sqrt{6}}}{3}$����2�֣�
��$b=1��a=\sqrt{2}$����3�֣�
���������Բ���̣�$\frac{x^2}{2}+{y^2}=1$����4�֣�
��2��$\left\{{\begin{array}{l}{\frac{x^2}{2}+{y^2}=1}\\{y=kx+m}\end{array}}\right.$��y�����ã�$��\frac{1}{2}+{k^2}��{x^2}+2kmx+{m^2}-1=0$����6�֣�
��C��x1��y1����D��x2��y2����CD�����E��x0��y0����
��${x_0}=-\frac{km}{{\frac{1}{2}+{k^2}}}��{y_0}=k{x_0}+m$������7�֣�
${k_{BE}}=\frac{{{y_0}+1}}{x_0}=-\frac{1}{k}$����8�֣�
����x0+ky0+k=0����1+k2��x0+km+k=0��
��$��1+{k^2}��•\frac{-km}{{\frac{1}{2}+{k^2}}}+km+k=0$��$\frac{{-m��1+{k^2}��}}{{\frac{1}{2}+{k^2}}}+m+1=0$��
��m=1+2k2����k��0����m��1������9�֣�
��$��={��2km��^2}-4��\frac{1}{2}+{k^2}����{m^2}-1����0$
��m2-��1+2k2����0������10�֣�
��m2-m��0��m�ʣ�0��1������11�֣�
����������������������ֱ�ߣ�����Բ�ڲ�ͬ�����㣬�������㶼����BΪԲ�ĵ�Բ�ϣ���12 ��
���� ���⿼����Բ���̵���ֱ������Բ��λ�ù�ϵ��Ӧ�ã�����������Ľ������������ת��˼���Լ�����������


 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{3}{2}$ | B�� | $��3\sqrt{2}$ | C�� | ��3 | D�� | $��\frac{3}{2}\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2��b2 | B�� | ab��b2 | C�� | a+b��0 | D�� | |a|+|b|��a+b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
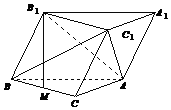 ��ͼ��б������ABC-A1B1C1�ĵ�����ֱ�������Σ���ACB=90�㣬M��BC���е㣬��BM1��BC��ƽ��B1C1CB��ƽ��ABC��BC=CA=AA1��
��ͼ��б������ABC-A1B1C1�ĵ�����ֱ�������Σ���ACB=90�㣬M��BC���е㣬��BM1��BC��ƽ��B1C1CB��ƽ��ABC��BC=CA=AA1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{3}{4}$ | D�� | $\frac{\sqrt{2}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {1��2} | B�� | {2��3} | C�� | {3��4} | D�� | {4��5} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���⡰?x��1��x2-1��0���ķ��ǡ�?x��1��x2-1��0�� | |
| B�� | ��x=2���ǡ�x2-x-2=0���ij�ֲ���Ҫ���� | |
| C�� | ����p��q��Ϊ�����⣬��p��q��Ϊ������ | |
| D�� | ���⡰��a•b=0����a=0��b=0���ķ�����Ϊ����a•b��0����a��0��b��0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
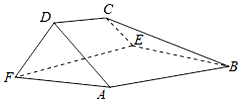 ��ͼ������A��B��C��D��E��FΪ������������У���ABEFΪ�����Σ�AF=2FD����AFD=90�㣬�Ҷ����D-AF-E������C-BE-F����60�㣮
��ͼ������A��B��C��D��E��FΪ������������У���ABEFΪ�����Σ�AF=2FD����AFD=90�㣬�Ҷ����D-AF-E������C-BE-F����60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a=-5��a=-15 | B�� | a=-5��a=15 | C�� | a=5��a=-15 | D�� | a=5��a=15 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com