
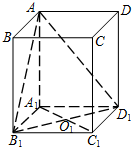
 已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1是A1C1和B1D1的交点.
已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1是A1C1和B1D1的交点.分析 (1)由题意,正四棱柱ABCD-A1B1C1D1是棱长为1的正方体,连结AO1,则∠AO1A1是二面角A-B1D1-A1的平面角,由此能求出二面角A-B1D1-A1的大小.
(2)设正四棱柱的高为h,以A1为原点,A1B1为x轴,A1D1为y轴,A1A为z轴,建立空间直角坐标系,利用向量法能求出正四棱柱ABCD-A1B1C1D1的高.
解答 解:(1)由题意,正四棱柱ABCD-A1B1C1D1是棱长为1的正方体,…(1分)
连结AO1,因为AB1=AD1,O1为B1D1的中点,所以AO1⊥B1D1,…(2分)
又A1C1⊥B1D1,所以∠AO1A1是二面角A-B1D1-A1的平面角. …(3分)
因为AA1⊥平面A1B1C1D1,所以AA1⊥A1C1,…(4分)
所以,$tan∠A{O_1}{A_1}=\frac{{A{A_1}}}{{{A_1}{O_1}}}=\sqrt{2}$. …(5分)
所以,二面角A-B1D1-A1的大小为$arctan\sqrt{2}$.…(6分)
(2)设正四棱柱的高为h.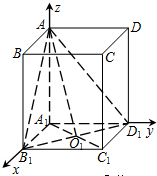
如图以A1为原点,A1B1为x轴,A1D1为y轴,A1A为z轴,建立空间直角坐标系,
则A(0,0,h),B1(1,0,0),D1(0,1,0),C(1,1,h),
$\overrightarrow{A{B_1}}=(1\;,\;0\;,\;-h)$,$\overrightarrow{A{D_1}}=(0\;,\;1\;,\;-h)$,$\overrightarrow{AC}=(1\;,\;1\;,\;0)$. …(2分)
设平面AB1D1一个法向量为$\vec n=(x\;,\;y\;,\;z)$,
由$\left\{\begin{array}{l}\vec n⊥\overrightarrow{A{B_1}}\;\\ \vec n⊥\overrightarrow{A{D_1}}\;\end{array}\right.$得$\left\{\begin{array}{l}\vec n•\overrightarrow{A{B_1}}=0\;\\ \vec n•\overrightarrow{A{D_1}}=0\;\end{array}\right.$即$\left\{\begin{array}{l}{x-hz=0}\\{y-hz=0}\end{array}\right.$,
取x-hx=h,得$\vec n=(h\;,\;h\;,\;1)$,…(5分)
所以,点C以平面AB1D1的距离为$d=\frac{{|\vec n•\overrightarrow{AC}|}}{|\vec n|}=\frac{2h}{{\sqrt{2{h^2}+1}}}=\frac{4}{3}$,
解得h=2.…(7分)
所以,正四棱柱ABCD-A1B1C1D1的高为2. …(8分)
点评 本题考查二面角的大小的求法,考查正四棱柱的高的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
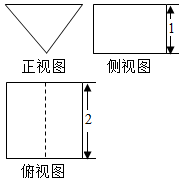 一个多面体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该多面体的表面积为( )
一个多面体的三视图如图所示,正视图为等腰直角三角形,俯视图中虚线平分矩形的面积,则该多面体的表面积为( )| A. | 2 | B. | 4+2$\sqrt{2}$ | C. | 4+4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
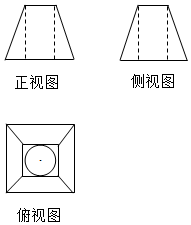 已知一个几何体的三视图如图所示,正视图和侧视图是两个的全等的等腰梯形,梯形上底、下底分别为2,4,腰长为$\sqrt{10}$,则该几何体的体积为( )
已知一个几何体的三视图如图所示,正视图和侧视图是两个的全等的等腰梯形,梯形上底、下底分别为2,4,腰长为$\sqrt{10}$,则该几何体的体积为( )| A. | $\frac{28}{3}$$\sqrt{10}$-3π | B. | 28-2π | C. | 28-3π | D. | $\frac{28}{3}$$\sqrt{10}$-2π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com