
己知函数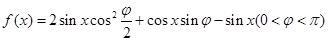 在
在 处取最小值.
处取最小值.
(1)求 的值。
的值。
(2)在△ABC中,a、b、c分别是A、B、C的对边,已知a=l,b=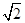 ,
,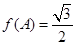 ,求角C.
,求角C.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C对应的边分别是a,b,c.已知cos2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(3)是否存在v,使得小艇以v海里/时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
△ABC为一个等腰三角形形状的空地,腰AC的长为3(百米),底AB的长为4(百米).现决定在空地内筑一条笔直的小路EF(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等,面积分别为S1和S2.
(1)若小路一端E为AC的中点,求此时小路的长度;
(2)若小路的端点E、F两点分别在两腰上,求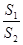 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,向量m=(1,cosB),n=(sinB,- ),且m⊥n.
),且m⊥n.
(1)求角B的大小.
(2)若△ABC的面积为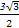 ,a=2,求b的值.
,a=2,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A- sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.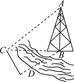
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com