
【题目】如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.

(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的单调函数f(x)满足对任意的x1 , x2 , 都有f(x1+x2)=f(x1)+f(x2)成立.若正实数a,b满足f(a)+f(2b﹣1)=0,则 ![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
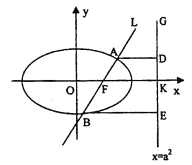
【题目】如图,已知直线![]() 的右焦点
的右焦点![]() ,且交椭圆
,且交椭圆![]() 于
于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影依次为点
上的射影依次为点![]() .
.
(Ⅰ)已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的上顶点。
的上顶点。
①求椭圆![]() 的方程;
的方程;
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() ,当
,当![]() 变化时,求
变化时,求![]() 的值;
的值;
(Ⅱ)连接![]() ,试探索当
,试探索当![]() 变化时,直线
变化时,直线![]() 是否相交于一定点
是否相交于一定点![]() ?若交于定点
?若交于定点![]() ,请求出
,请求出![]() 点的坐标并给予证明;否则说明理由.
点的坐标并给予证明;否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.规定:成绩不低于120分时为优秀成绩. 
(1)从甲班的样本中有放回的随机抽取 2 个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名同学的成绩,记获优秀成绩的人数为ξ,求ξ的分布列和数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]() 内是单调函数;②
内是单调函数;②![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的“倍值区间”.下列函数中存在“倍值区间”的有_______
的“倍值区间”.下列函数中存在“倍值区间”的有_______
①![]() ②
②![]() ③
③![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有一个三边长分别为3,4,5的三角形.求下面两只蚂蚁与三角形三顶点的距离均超过1的概率.(1)一只蚂蚁在三角形的边上爬行(2)一只蚂蚁在三角形所在区域内部爬行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com