
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
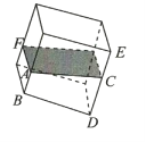
【答案】(1)可以是矩形,但不可能是其他非矩形的平行四边形(2)水比较少时,是三棱柱,水多时,可能是四棱柱,或五棱柱;但不可能是棱台或棱锥.(3)(1)对,(2)不对.
【解析】
根据绕着棱旋转和绕着点旋转的特点,将问题转化为长方体被相应平面所截形成的截面形状.
(1)不对.水面的形状就是用一个与棱(长方体容器倾斜时固定不动的棱)平行的平面截长方体时截面的形状,因而可以是矩形,但不可能是其他非矩形的平行四边形.
(2)不对.水的形状就是用与棱(长方体容器倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余部分的几何体,此几何体是棱柱,水比较少时,是三棱柱,水多时,可能是四棱柱,或五棱柱;但不可能是棱台或棱锥.
(3)用任意一个平面去截长方体,其截面形状可以是三角形,四边形,五边形,六边形,因而水面的形状可以是三角形,四边形,五边形,六边形;水的形状可以是棱锥,棱柱,但不可能是棱台.故(1)对,(2)不对.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地区现有一个直角梯形水产养殖区ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在点P处有一灯塔(如图),且点P到BC,CD的距离都是1200m,现拟将养殖区ACD分成两块,经过灯塔P增加一道分隔网EF,在△AEF内试验养殖一种新的水产品,当△AEF的面积最小时,对原有水产品养殖的影响最小.设AE=d.
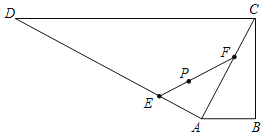
(1)若P是EF的中点,求d的值;
(2)求对原有水产品养殖的影响最小时的d的值,并求△AEF面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对于定义域内的任意实数
,对于定义域内的任意实数![]() ,有
,有![]() 成立,且
成立,且![]() 时,
时,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(3)已知![]() (实数
(实数![]() ),求实数
),求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图表示一位骑自行车者和一位骑摩托车者在相距![]() 的两城镇间旅行的函数图象,由图,可知骑自行车者用了
的两城镇间旅行的函数图象,由图,可知骑自行车者用了![]() ,沿途休息了
,沿途休息了![]() ,骑摩托车者用了
,骑摩托车者用了![]() ,根据这个图象,提出关于这两个旅行者的如下信息:
,根据这个图象,提出关于这两个旅行者的如下信息:

①骑自行车者比骑摩托车者早出发![]() ,晚到
,晚到![]() ;
;
②骑自行车者是变速运动,骑摩托者是匀速运动;
③骑摩托车者在出发了![]() 后,追上了骑自行车者.
后,追上了骑自行车者.
其中正确信息的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.![]() 是自然对数的底数.
是自然对数的底数.
(1)若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .求实数
.求实数![]() 的值;
的值;
(2)① 若![]() 时,函数
时,函数![]() 既有极大值,又有极小值,求实数
既有极大值,又有极小值,求实数![]() 的取值范围;
的取值范围;
② 若![]() ,
,![]() .若
.若![]() 对一切正实数
对一切正实数![]() 恒成立,求实数
恒成立,求实数![]() 的最大值(用
的最大值(用![]() 表示).
表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}(an∈Z)的前n项和为Sn,记S1,S2,…,Sn中奇数的个数为bn.
(1)若an=n,请写出数列{bn}的前5项;
(2)求证:“a1为奇数,ai(i=2,3,4,…)为偶数”是“数列{bn}是单调递增数列”的充分不必要条件;
(3)若ai=bi,i=1,2,3,…,求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com