
(1)试判断函数f(x)的单调性,并给出证明;
(2)解关于x的不等式f[x(x-1)]<![]() .
.
解:(1)定义域中的x必须满足
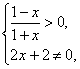
解得-1<x<1.
∴函数f(x)的定义域为(-1,1).
任取-1<x1<x2<1,则
f(x2)-f(x1)
=(![]()
∵-1<x1<x2<1,
∴![]() <0,(1-x2)(1+x1)>0,
<0,(1-x2)(1+x1)>0,
(1+x2)(1-x1)>0,
(1-x2)(1+x1)-(1+x2)(1-x1)=2(x1-x2)<0.
∴0<![]() <1.
<1.
从而lg![]() <0.
<0.
于是,f(x2)-f(x1)<0,即f(x2)<f(x1).故函数f(x)在(-1,1)上是减函数.
(2)∵f(0)=![]() ,∴f[x(x-1)]<f(0).
,∴f[x(x-1)]<f(0).
又∵f(x)在(-1,1)上单调递减,∴0<x(x-1)<1.
解得![]() <x<0或1<x<
<x<0或1<x<![]() .
.
故所求不等式的解集是(![]() ,0)∪(1,
,0)∪(1,![]() ).
).


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
|
| (a+b)-(a-b)f(a-b) |
| 2 |
| A、a | B、b |
| C、a,b中较小的数 | D、a,b中较大的数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x |
| 1+x |
A、-
| ||
B、-
| ||
| C、-1 | ||
| D、-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、a<0 | B、0≤a<1 |
| C、a=1 | D、a>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com