
| A. | ①和②均为真命题 | B. | ①为真命题,②为假命题 | ||
| C. | ①为假命题,②为真命题 | D. | ①和②均为假命题 |
分析 对函数$f(x)=-x+2\sqrt{x}$,G(x)=$\frac{-x+2\sqrt{x}}{x}=\frac{2}{\sqrt{x}}-1$在(0,1)上的单调性进行判断,得命题①是真命题.对函数$g(x)=\frac{2x}{{1-{x^2}}}$=$\frac{2}{\frac{1}{x}-x}$,H(x)=$\frac{g(x)}{x}=\frac{1}{1-{x}^{2}}$在(0,1)上单调性进行判断,得命题②是假命题.
解答 解:对于命题①:令t=$\sqrt{x}$,函数$f(x)=-x+2\sqrt{x}$=-t2+2t,∵t=$\sqrt{x}$在(0,1)上是增函数,
函数y=-t2+2t在(0,1)上是增函数,∴在(0,1)上是增函数;
G(x)=$\frac{-x+2\sqrt{x}}{x}=\frac{2}{\sqrt{x}}-1$在(0,1)上是减函数,
∴函数$f(x)=-x+2\sqrt{x}$是(0,1)上的“H函数“,故命题①是真命题.
对于命题②,函数$g(x)=\frac{2x}{{1-{x^2}}}$=$\frac{2}{\frac{1}{x}-x}$是(0,1)上的增函数,H(x)=$\frac{g(x)}{x}=\frac{1}{1-{x}^{2}}$是(0,1)上的增函数,故命题②是假命题;
故选:B.
点评 本题考查了命题真假的判定,涉及到了函数的单调性,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:解答题
 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
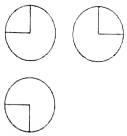 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,半径长度为2,则该几何体的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-2)>f(0)>f(1) | B. | f(-2)>f(1)>f(0) | C. | f(1)>f(0)>f(-2) | D. | f(1)>f(-2)>f(0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com