
分析 (1)利用等差数列的通项公式与求和公式即可得出.
(2)利用“裂项求和”方法即可得出.
解答 解:(1)∵λ,6,3λ成等差数列,∴λ+3λ=12,∴λ=3.
∴等差数列{an}的首项为3,公差d=3,
前n项和公式Sn=$3n+\frac{n(n-1)}{2}×3$=$\frac{3{n}^{2}+3n}{2}$,
由Sk=165,可得3k+$\frac{3k(k-1)}{2}$=165,解得k=10.
(2)∵bn=$\frac{3}{2{S}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$,
∴数列{bn}的前n项和Tn=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$.
点评 本题考查了等差数列的通项公式与求和公式、“裂项求和”,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
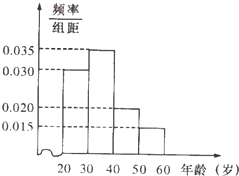 某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.
某工厂有120名工人,其年龄都在20~60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60)分成四组,其频率分布直方图如图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试.已知各年龄段两项培训结业考试成绩优秀的人数如表所示.假设两项培训是相互独立的,结业考试也互不影响.| 年龄分组 | A项培训成绩优秀人数 | B项培训成绩优秀人数 |
| [20,30) | 27 | 16 |
| [30,40) | 28 | 18 |
| [40,50) | 26 | 9 |
| [50,60] | 6 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4\sqrt{3}}{3}$ | B. | $\frac{16\sqrt{3}}{3}$ | C. | $\frac{32\sqrt{3}}{3}$ | D. | $\frac{64\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$或$\frac{5π}{6}$ | B. | $-\frac{π}{3}$或$\frac{π}{3}$ | C. | $-\frac{π}{6}$或$\frac{π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x>1,则?y∈(-∞,1),xy≠1 | B. | 若x=sinθcosθ,则?θ∈(0,π),x≠$\frac{1}{2}$ | ||
| C. | 若x>1,则?y∈(-∞,1),xy=1 | D. | 若x=sinθcosθ,则?θ∈(0,π),x=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com