
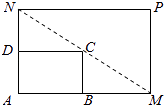
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过点C,已知AB=3米,AD=2米,记矩形AMPN的面积为S平方米. 
(1)按下列要求建立函数关系;
(i)设AN=x米,将S表示为x的函数;
(ii)设∠BMC=θ(rad),将S表示为θ的函数.
(2)请你选用(1)中的一个函数关系,求出S的最小值,并求出S取得最小值时AN的长度.
【答案】
(1)解:(i)∵Rt△CDN~Rt△MBC,∴ ![]() =
= ![]() ,
,
∴ ![]() ,∴BM=
,∴BM= ![]() ,
,
由于 ![]() ,则AM=
,则AM= ![]()
∴S=ANAM= ![]() ,(x>2)
,(x>2)
(ii)在Rt△MBC中,tanθ= ![]() ,∴MB=
,∴MB= ![]() ,∴AM=3+
,∴AM=3+ ![]() ,
,
在Rt△CDN中,tanθ= ![]() ,∴DN=3tanθ,∴AN=2+3tanθ,
,∴DN=3tanθ,∴AN=2+3tanθ,
∴S=AMAN=(3+ ![]() )(2+3tanθ),其中0<θ<
)(2+3tanθ),其中0<θ< ![]()
(2)解:选择(ii)中关系式
∵S=AMAN=(3+ ![]() )(2+3tanθ),(0<θ<
)(2+3tanθ),(0<θ< ![]() );
);
∴S=12+9tanθ+ ![]() ≥12+2
≥12+2 ![]() =24,
=24,
当且仅当9tanθ= ![]() ,即tanθ=
,即tanθ= ![]() 时,取等号,此时AN=4
时,取等号,此时AN=4
答:当AN的长度为4米时,矩形AMPN的面积最小,最小值为24m2.
【解析】(1)求出AN,AM,即可建立函数关系;(i)设AN=x米,先求出AM的长,即可表示出矩形AMPN的面积;(ii)由∠BMC=θ(rad),可以依次表示出AM与AN的长度,即可表示出S关于θ的函数表达式;(2)选择(ii)中的函数关系式,化简,由基本不等式即可求出最值.
【考点精析】利用基本不等式在最值问题中的应用对题目进行判断即可得到答案,需要熟知用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
,![]() 的数据).
的数据).
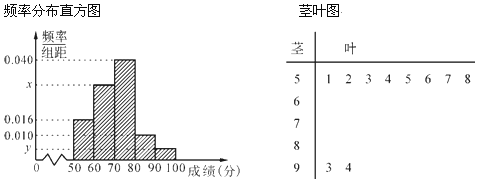
(1)求样本容量n和频率分布直方图中x、y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的2名同学来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1 , 设AB1的中点为D,B1C∩BC1=E. 
求证:
(1)DE∥平面AA1C1C;
(2)BC1⊥AB1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+2ax(a为常数)的图象与y轴交于点A,曲线y=f(x)在点A处的切线斜率为﹣1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2+1<ex .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费支出x与销售额y(单位:万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com