
| A. | $\frac{1023}{1024}$ | B. | $\frac{1025}{1024}$ | C. | $\frac{2047}{2048}$ | D. | $\frac{2049}{2048}$ |
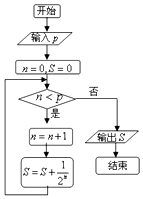
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{9}}$的和,由等比数列的前n项和公式计算可得答案.
解答 解:由程序框图可知:
S=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{9}}$=$\frac{\frac{1}{2}[1{-(\frac{1}{2})}^{9}]}{1-\frac{1}{2}}$=$\frac{1023}{1024}$,
故选:A.
点评 作这类题的关键是看懂其算法过程.把程序语言翻译成代数去处理求值.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
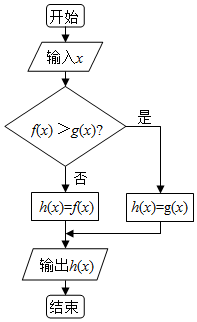
| A. | 2016 | B. | 2017 | C. | logπ2016 | D. | ln2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
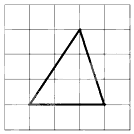
| A. | $\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{9}{2}$ | D. | $\frac{9}{2}\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{12}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | C. | $\frac{x^2}{4}+{y^2}=1$ | D. | $\frac{x^2}{2}+{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=$\sqrt{3}$AD,AE⊥PC于点E,EF∥CD,交PD于点F
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD=$\sqrt{3}$AD,AE⊥PC于点E,EF∥CD,交PD于点F查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com