
【题目】已知函数![]() (
(![]() ),且满足
),且满足![]() .
.
(1)求a的值;
(2)设函数![]() ,
,![]() (
(![]() ),若存在
),若存在![]() ,
,![]() ,使得
,使得![]() 成立,求实数t的取值范围;
成立,求实数t的取值范围;
(3)若存在实数m,使得关于x的方程![]() 恰有4个不同的正根,求实数m的取值范围.
恰有4个不同的正根,求实数m的取值范围.
【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意,代入函数值,即可求解;
(2)根据题意,求解函数![]() 和
和![]() 值域,若存在
值域,若存在![]() ,
,![]() ,使得
,使得![]() 成立,转化为值域有交集,即可求解参数取值范围;
成立,转化为值域有交集,即可求解参数取值范围;
(3)由(1)分析函数![]() 的值域,可知
的值域,可知![]() 时,
时,![]() 有两根;再观察方程,同除
有两根;再观察方程,同除![]() 后方程可化简为
后方程可化简为![]() ,只需使方程在
,只需使方程在![]() 上有两根,即可求解.
上有两根,即可求解.
(1)由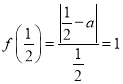 ,得
,得![]() 或0.
或0.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)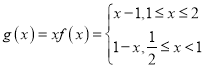 ,
,
所以![]() ;故
;故![]() 的值域为
的值域为![]()
因为![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
所以![]() 的值域为
的值域为![]() ,由题意
,由题意![]() ,
,
考虑到![]() ,所以
,所以![]() ,解得
,解得![]() ;
;
综上:实数t的取值范围是![]()
(3)当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数;
上为增函数;
当![]() 时,
时,![]() .
.
可得![]() 在
在![]() 上为减函数,当
上为减函数,当![]() 时,
时,![]() .
.
方程![]() 可化为
可化为![]() ,
,
即![]() .
.
设![]() ,方程可化为
,方程可化为![]() .
.
要使原方程有4个不同的正根,
则关于s方程![]() 在
在![]() 有两个不等的根
有两个不等的根![]() ,
,![]() ,
,
则有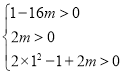 ,解得
,解得![]() ,
,
所以实数m的取值范围为![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】幻彩摩天轮位于中山市西区兴中广场C段4层高的建筑之上,与中山市第一家四星级酒店——富华酒店隔河相望,其外观是参考世界最高的摩天轮新加坡“飞行者”的设计,轮体上有36个吊舱,共可同时承载288人从高空俯瞰岐江一河两岸的美景.幻彩摩天轮直径为83m,每20min转一圈,最高点离地108m,摩天轮上的点P的起始位置在最低点处.已知在时刻t(min)时P距离地面的高度![]() ,(其中
,(其中![]() ),
),
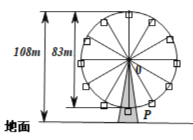
(1)求![]() 的函数解析式.
的函数解析式.
(2)当离地面![]() m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
m以上时,可以俯瞰富华酒店顶楼,求转一圈中有多少时间可以俯瞰富华酒店顶楼?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() )的部分图象如图所示.
)的部分图象如图所示.
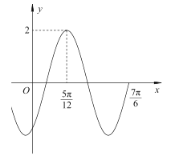
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的最小值及
的最小值及![]() 取到最小值时自变量x的集合;
取到最小值时自变量x的集合;
(3)将函数图像上所有点的纵坐标不变,横坐标变为原来的![]() (
(![]() )倍,得到函数
)倍,得到函数![]() 的图象.若函数
的图象.若函数![]() 在区间
在区间![]() 上恰有5个零点,求t的取值范围.
上恰有5个零点,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知△![]() 中,∠
中,∠![]() =90°,
=90°,![]() ,且
,且![]() =1,
=1,![]() =2,△
=2,△![]() 绕
绕![]() 旋转至
旋转至![]() ,使点
,使点![]() 与点
与点![]() 之间的距离
之间的距离![]() =
=![]() .
.
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求异面直线![]() 与
与![]() 所成的角的余弦值.
所成的角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:

(1)求频率直方图中a的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中人选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com