
设函数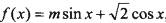 ,(w为常数,且m >0),已知函数f(x)的最大值为2.
,(w为常数,且m >0),已知函数f(x)的最大值为2.
(I)求函数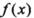 的单调递减区间;
的单调递减区间;
(II)已知a,b,c是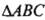 的三边,且
的三边,且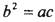 .若,
.若,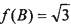 ,求B的值.
,求B的值.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| x |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() ,
,![]() 为常数).当
为常数).当![]() 时,
时,![]() ,且
,且![]() 为
为![]() 上的奇函数.
上的奇函数.
(Ⅰ)若![]() ,且
,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;w.w.w.k.s.5.u.c.o.m
的表达式;w.w.w.k.s.5.u.c.o.m
(Ⅱ)在(Ⅰ)的条件下,![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交![]() 元(
元(![]() 为常数,
为常数,![]() )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为![]() 元(
元(![]() ),根据市场调查,日销售量与
),根据市场调查,日销售量与![]() (
(![]() 为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润
为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。w.w.w求商店的日利润![]() 元与每件产品的日售价
元与每件产品的日售价![]() 元的函数关系式;当每件产品的日售价为多少元时该商店的日利润
元的函数关系式;当每件产品的日售价为多少元时该商店的日利润![]() 最大,说明理由。
最大,说明理由。
查看答案和解析>>
科目:高中数学 来源:2011届广东省高三高考全真模拟试卷数学文卷二 题型:解答题
(本小题满分14分)某商店经销一种广州亚运会纪念品,每件产品成本为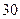 元,且每卖出一件产品,需向税务部门上交
元,且每卖出一件产品,需向税务部门上交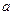 元(
元(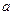 为常数,
为常数,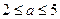 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为 元(
元(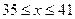 ),根据市场调查,日销售量与
),根据市场调查,日销售量与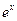 (
(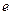 为自然对数的底数)成反比,已知每件产品的日售价为
为自然对数的底数)成反比,已知每件产品的日售价为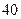 元,日销售量为
元,日销售量为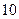 件。w.w.w..c.o.m
件。w.w.w..c.o.m
(1)求商店的日利润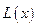 元与每件产品的日售价
元与每件产品的日售价 元的函数关系式;
元的函数关系式;
(2)当每件产品的日售价为多少时该商店的日利润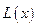 最大,说明理由.
最大,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com