
【题目】已知数列{an}满足an=3an﹣1+3n﹣1(n∈N*,n≥2)且a3=95.
(1)求a1 , a2的值;
(2)求实数t,使得bn= ![]() (an+t)(n∈N*)且{bn}为等差数列;
(an+t)(n∈N*)且{bn}为等差数列;
(3)在(2)条件下求数列{an}的前n项和Sn .
【答案】
(1)解:当n=2时,a2=3a1+8,
当n=3时,a3=3a3+33﹣1=95,
∴a2=23,
∴23=3a1+8,
∴a1=5
(2)解:当n≥2时,bn﹣bn﹣1= ![]() (an+t)﹣
(an+t)﹣ ![]() (an﹣1+t)=
(an﹣1+t)= ![]() (an+t﹣3an﹣1﹣3t)=
(an+t﹣3an﹣1﹣3t)= ![]() (3n﹣1﹣2t).
(3n﹣1﹣2t).
要使{bn}为等差数列,则必须使1+2t=0,
∴t=﹣ ![]() ,
,
即存在t=﹣ ![]() ,使数列{bn}为等差数列
,使数列{bn}为等差数列
(3)解:∵当t=﹣ ![]() ,时,数列{bn}为等差数列,且bn﹣bn﹣1=1,b1=
,时,数列{bn}为等差数列,且bn﹣bn﹣1=1,b1= ![]() ,
,
∴bn= ![]() +(n﹣1)=n+
+(n﹣1)=n+ ![]() ,
,
∴an=(n+ ![]() )3n+
)3n+ ![]() ,
,
于是,Sn= ![]() ×3+
×3+ ![]() 32+…+
32+…+ ![]() 3n+
3n+ ![]() ×n,
×n,
令S=3×3+5×32+…+(2n+1)3n,①
3S=3×32+5×33+…+(2n+1)3n+1,②
①﹣②得﹣2S=3×3+3×32+2×33+…+23n﹣(2n+1)3n+1,②
化简得S=n3n+1,
∴Sn= ![]() +
+ ![]() =
= ![]() ,
,
数列{an}的前n项和Sn,Sn= ![]()
【解析】(1)当n=2时,a2=3a1+8,当n=3时,a3=3a3+33﹣1=95,可得a2=23,代入即可求得a1=5;(2)由等差数列的性质可知:bn﹣bn﹣1= ![]() (an+t)﹣
(an+t)﹣ ![]() (an﹣1+t)=
(an﹣1+t)= ![]() (an+t﹣3an﹣1﹣3t)=
(an+t﹣3an﹣1﹣3t)= ![]() (3n﹣1﹣2t).可知:1+2t=0,即可求得t的值;(3)由等差数列的通项公式可得bn=
(3n﹣1﹣2t).可知:1+2t=0,即可求得t的值;(3)由等差数列的通项公式可得bn= ![]() +(n﹣1)=n+
+(n﹣1)=n+ ![]() ,求得an=(n+
,求得an=(n+ ![]() )3n+
)3n+ ![]() ,采用分组求和及“错位相减法”即可求得数列{an}的前n项和Sn .
,采用分组求和及“错位相减法”即可求得数列{an}的前n项和Sn .
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() ,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系
,以及对数列的前n项和的理解,了解数列{an}的前n项和sn与通项an的关系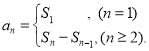 .
.


科目:高中数学 来源: 题型:
【题目】微信已成为人们常用的社交软件,“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的![]() 或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
或点赞.现从小明的微信朋友圈内随机选取了40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0 | 2001 | 5001 | 8001 | >10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
若某人一天的走路步数超过8000步被系统评定为“积极型”,否则被系统评定为“懈怠型”.
(1)利用样本估计总体的思想,试估计小明的所有微信好友中每日走路步数超过10000步的概率;
(2)根据题意完成下面的![]() 列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有90%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: 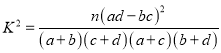
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:①y=1是幂函数;
②定义在R上的奇函数y=f(x)满足f(0)=0
③函数 ![]() 是奇函数
是奇函数
④当a<0时, ![]()
⑤函数y=1的零点有2个;
其中正确结论的序号是(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(a,b)(ab≠0)是圆x2+y2=r2内的一点,直线m是以P为中点的弦所在直线,直线l的方程为ax+by=r2 , 那么( )
A.m∥l,且l与圆相交
B.m⊥l,且l与圆相切
C.m∥l,且l与圆相离
D.m⊥l,且l与圆相离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙C经过点A(﹣2,0),B(0,2),且圆心C在直线y=x上,直线L:y=kx+1与⊙C相交于P,Q点.
(1)求⊙C的方程.
(2)过点(0,1)作直线L1⊥L,且L1交⊙C于M,N,求四边形PMQN的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(2,0),点B(﹣2,0),直线l:(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R).
(1)求直线l所经过的定点P的坐标;
(2)若直线l与线段AB有公共点,求λ的取值范围;
(3)若分别过A,B且斜率为 ![]() 的两条平行直线截直线l所得线段的长为4
的两条平行直线截直线l所得线段的长为4 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com