
【题目】对于![]() 维向量
维向量![]() ,若对任意
,若对任意![]() 均有
均有![]() 或
或![]() ,则称
,则称![]() 为
为![]() 维
维![]() 向量. 对于两个
向量. 对于两个![]() 维
维![]() 向量
向量![]() 定义
定义![]() .
.
(1)若![]() , 求
, 求![]() 的值;
的值;
(2)现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,求证:该序列中不存在
,求证:该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(3) 现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,若存在正整数
,若存在正整数![]() 使得
使得![]() 为
为![]() 维
维![]() 向量序列中的项,求出所有的
向量序列中的项,求出所有的![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在四个函数y=sin|x|,y=cos|x|,y= ![]() ,y=lg|sinx|中,以π为周期,在
,y=lg|sinx|中,以π为周期,在 ![]() 上单调递增的偶函数是( )
上单调递增的偶函数是( )
A.y=sin|x|
B.y=cos|x|
C.y= ![]()
D.y=lg|sinx|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,曲线
,曲线![]() 上的任意一点
上的任意一点![]() 满足:
满足: ![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
, ![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,设
点,设![]() ,
, ![]() ,试问
,试问![]() 是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
是否为定值?如果是定值,请求出这个定值,如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断其真假:
(1)p:不论m取何实数,方程x2+x-m=0必有实数根;
(2)q:存在一个实数x,使得x2+x+1≤0;
(3)r:等圆的面积相等,周长相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园,根据旅游局统计数据,该主題公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比, ![]() 以下为舒适,
以下为舒适, ![]() 为一般,
为一般, ![]() 以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览
以上为拥挤),情况如图所示,小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览![]() 天.
天.
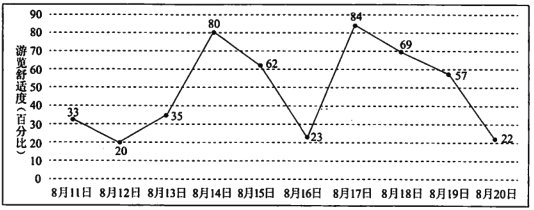
(1)求小明连续两天都遇上拥挤的概率;
(2)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某颜料公司生产![]() 两种产品,其中生产每吨
两种产品,其中生产每吨![]() 产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨
产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨![]() 产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果
产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果![]() 产品的利润为300元/吨,
产品的利润为300元/吨, ![]() 产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
A. 14000元 B. 16000元 C. 18000元 D. 20000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com