
【题目】设 ![]() 是定义在实数集
是定义在实数集 ![]() 上的函数,满足条件
上的函数,满足条件 ![]() 是偶函数,且当
是偶函数,且当 ![]() 时,
时, ![]() ,则
,则 ![]() ,
, ![]() ,
, ![]() 的大小关系是( )
的大小关系是( )
A.![]()
B.![]()
C.![]()
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知不等式|x+3|﹣2x﹣1<0的解集为(x0 , +∞)
(Ⅰ)求x0的值;
(Ⅱ)若函数f(x)=|x﹣m|+|x+ ![]() |﹣x0(m>0)有零点,求实数m的值.
|﹣x0(m>0)有零点,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过定点P(1,1),且倾斜角为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴的坐标系中,曲线C的极坐标方程为 ![]() .
.
(1)求曲线C的直角坐标方程与直线l的参数方程;
(2)若直线l与曲线C相交于不同的两点A,B,求|AB|及|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某工厂开展群众体育活动的情况,拟采用分层抽样的方法从A,B,C三个区中抽取7个工厂进行调查,已知A,B,C区中分别有18,27,18个工厂
(Ⅰ)求从A,B,C区中分别抽取的工厂个数;
(Ⅱ)若从抽取的7个工厂中随机抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自A区的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.命题“若 ![]() ,则
,则 ![]() ”的逆否命题为:“若
”的逆否命题为:“若 ![]() ,则
,则 ![]() ”
”
B.“ ![]() ”是“
”是“ ![]() ”的充分不必要条件
”的充分不必要条件
C.若 ![]() 且
且 ![]() 为假命题,则
为假命题,则 ![]() 、
、 ![]() 均为假命题
均为假命题
D.命题 ![]() :“
:“ ![]() ,使得
,使得 ![]() ”,则
”,则 ![]() :“
:“ ![]() ,均有
,均有 ![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数为( )
①“x∈R都有x2≥0”的否定是“x0∈R使得x02≤0”;
②“x≠3”是“|x|≠3”成立的充分条件;
③命题“若m≤ ![]() ,则方程mx2+2x+2=0有实数根”的否命题为真命题.
,则方程mx2+2x+2=0有实数根”的否命题为真命题.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂对新研发的一种产品进行试销,得到如下数据表:
(1)根据上表求出回归直线方程 ![]() ,并预测当单价定为8.3元时的销量;
,并预测当单价定为8.3元时的销量;
(2)如果该工厂每件产品的成本为5.5元,利用所求的回归方程,要使得利润最大,单价应该定为多少?
附:线性回归方程 ![]() 中斜率和截距最小二乘估计计算公式:
中斜率和截距最小二乘估计计算公式: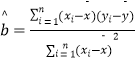 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若 ![]() ,则
,则 ![]() 或
或 ![]() ;
;
② ![]() ,都有
,都有 ![]() ;
;
③若 ![]() 是实数,则
是实数,则 ![]() 是
是 ![]() 的充分不必要条件;
的充分不必要条件;
④“ ![]() ” 的否定是“
” 的否定是“ ![]() ” ;
” ;
其中真命题的个数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com