
【题目】已知关于![]() 的不等式
的不等式![]() .
.
(1)当![]() 时,解不等式;
时,解不等式;
(2)如果不等式的解集为空集,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)当![]() 时,不等式
时,不等式![]() 变为
变为![]() 。由绝对值的意义,按绝对值号内的
。由绝对值的意义,按绝对值号内的![]() 的正负,分三种情况讨论:当
的正负,分三种情况讨论:当![]() 时,不等式变为
时,不等式变为![]() ;当
;当![]() 时,不等式变为
时,不等式变为![]() ,恒成立,所以
,恒成立,所以![]() 符合不等式;当
符合不等式;当![]() 时,不等式变为
时,不等式变为![]() 。取三种情况的并集,可得原不等式的解集。(2)解法一:构造函数
。取三种情况的并集,可得原不等式的解集。(2)解法一:构造函数![]() 与
与![]() ,原不等式的解集为空集,
,原不等式的解集为空集, ![]() 的最小值比大于或等于
的最小值比大于或等于![]() ,作出
,作出![]() 与
与![]() 的图象. 只须
的图象. 只须![]() 的图象在
的图象在![]() 的图象的上方,或
的图象的上方,或![]() 与
与![]() 重合,
重合, ![]() 。解法二:构造函数
。解法二:构造函数![]() ,讨论绝对值号内式子得正负去掉绝对值可得,
,讨论绝对值号内式子得正负去掉绝对值可得, ![]()
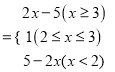 ,求每一段函数的值域,可得函数的最小值
,求每一段函数的值域,可得函数的最小值![]() =1,
=1, ![]() 小于等于函数的最小值1.解法三,由不等式
小于等于函数的最小值1.解法三,由不等式![]() 可得
可得![]() ,当且仅当
,当且仅当![]() 时,上式取等号,∴
时,上式取等号,∴![]() .
.
试题解析:解:(1)原不等式变为![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() ,∴
,∴ ![]()
当![]() 时,原不等式化为
时,原不等式化为![]() ,∴
,∴ ![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ,解得
,解得![]() ,∴
,∴ ![]() .
.
综上,原不等式解集为![]() .
.
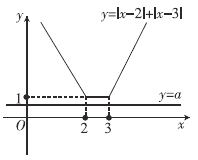
(2)解法一:作出![]() 与
与![]() 的图象.
的图象.
若使![]() 解集为空集,
解集为空集,
只须![]() 的图象在
的图象在![]() 的图象的上方,或
的图象的上方,或![]() 与
与![]() 重合,
重合,
∴![]() ,所以
,所以![]() 的范围为
的范围为![]() .
.
解法二: ![]()
 ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
综上![]() ,原问题等价于
,原问题等价于![]() ,∴
,∴ ![]() .
.
解法三:∵![]() ,当且仅当
,当且仅当![]() 时,上式取等号,∴
时,上式取等号,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
(1)命题![]() ,使得
,使得![]() ,则
,则![]() ,都有
,都有![]() ;
;
(2)已知函数f(x)=|log2x|,若a≠b,且f(a)=f(b),则ab=1;
(3)若平面α内存在不共线的三点到平面β的距离相等,则平面α平行于平面β;
(4)已知定义在![]() 上的函数
上的函数![]() 满足条件
满足条件![]() ,且函数
,且函数![]() 为奇函数,则函数
为奇函数,则函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
其中真命题的序号为______________.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() 为奇函数,a为常数,
为奇函数,a为常数,
(1)求a的值;
(2)证明f(x)在区间(1,+∞)上单调递增;
(3)若x∈[3,4],不等式f(x)>( ![]() )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+xlnx(a∈R)
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈Z时,不等式k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com