
【题目】已知向量a=![]() ,b=
,b=![]() ,且x∈
,且x∈![]() .
.
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-![]() ,求λ的值.
,求λ的值.
【答案】见解析
【解析】解 (1)a·b=cos ![]() cos
cos ![]() -sin
-sin ![]() sin
sin ![]() =cos 2x,
=cos 2x,
|a+b|=![]()
=![]() =2
=2![]() ,
,
因为x∈![]() ,所以cos x≥0,
,所以cos x≥0,
所以|a+b|=2cos x.
(2)由(1),可得f(x)=a·b-2λ|a+b|=cos 2x-4λcos x,
即f(x)=2(cos x-λ)2-1-2λ2.
因为x∈![]() ,所以0≤cos x≤1.
,所以0≤cos x≤1.
①当λ<0时,当且仅当cos x=0时,f(x)取得最小值-1,这与已知矛盾;
②当0≤λ≤1时,当且仅当cos x=λ时,f(x)取得最小值-1-2λ2,由已知得-1-2λ2=-![]() ,解得λ=
,解得λ=![]() ;
;
③当λ>1时,当且仅当cos x=1时,f(x)取得最小值1-4λ,由已知得1-4λ=-![]() ,解得λ=
,解得λ=![]() ,这与λ>1相矛盾;综上所述λ=
,这与λ>1相矛盾;综上所述λ=![]() .
.


科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下列命题:
有下列命题:
①函数![]() 的图象关于
的图象关于![]() 轴对称;
轴对称;
②在区间![]() 上,函数
上,函数![]() 是减函数;
是减函数;
③在区间![]() 上,函数
上,函数![]() 是增函数;
是增函数;
④函数![]() 的值域是
的值域是![]() .其中正确命题序号为____.
.其中正确命题序号为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求证: ![]() .
.
(2)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
sin213°+cos217°-sin13°cos17°;
sin215°+cos215°-sin15°cos15°;
sin218°+cos212°-sin18°cos12°;
sin2(-18°)+cos248°-sin(-18°)cos48°;
sin2(-25°)+cos255°-sin(-25°)cos55°.
①试从上述五个式子中选择一个,求出这个常数;
②根据①的计算结果,将该同学的发现推广为三角恒等式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 同时满足:①对于定义域上的任意
同时满足:①对于定义域上的任意![]() ,恒有
,恒有![]() ;②对于定义域上的任意
;②对于定义域上的任意![]() ,
, ![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则称函数
,则称函数![]() 为“理想函数”.在下列三个函数中:(1)
为“理想函数”.在下列三个函数中:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .“理想函数”有__________.(只填序号)
.“理想函数”有__________.(只填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,如果成年人按规定的剂量服用,据监测,服药后每毫升血液中的含药量![]() (微克)与时间
(微克)与时间![]() (小时)之间的关系近似满足如图所示的曲线.
(小时)之间的关系近似满足如图所示的曲线.
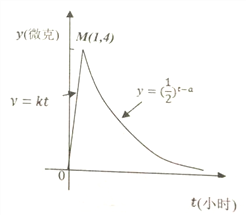
(1)写出服药后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效.求服药一次治疗疾病的有效时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .对于结论
.对于结论
(1)当![]() 时,
时, ![]() ;(2)函数
;(2)函数![]() 的零点个数可以为4,5,7;
的零点个数可以为4,5,7;
(3)若![]() ,关于
,关于![]() 的方程
的方程![]() 有5个不同的实根,则
有5个不同的实根,则![]() ;
;
(4)若函数![]() 在区间
在区间![]() 上恒为正,则实数
上恒为正,则实数![]() 的范围是
的范围是![]() .
.
说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,l是过定点P(4,2)且倾斜角为α的直线;在极坐标系(以坐标原点O为极点,
以x轴非负半轴为极轴,取相同单位长度)中,曲线C的极坐标方程为![]() .
.
(1)写出直线l的参数方程,并将曲线C的方程化为直角坐标方程;
(2)若曲线C与直线相交于不同的两点M,N,求|PM|+|PN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2-2x-3,求f(3),f(-5),f(5),并计算f(3)+f(-5)+f(5)的值.设计出解决该问题的一个算法,并画出程框图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com