
【题目】已知函数f(x)= ![]() 为偶函数.
为偶函数.
(1)求实数a的值;
(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=(lg 2)2+lg 2lg 5+lg 5﹣ ![]() ,判断λ与E的关系;
,判断λ与E的关系;
(3)当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
](m>0,n>0)时,若函数f(x)的值域为[2﹣3m,2﹣3n],求m,n的值.
【答案】
(1)解:函数f(x)= ![]() ,则f(﹣x)=
,则f(﹣x)= ![]() =
= ![]() ,
,
又由函数f(x)为偶函数,则有f(﹣x)=f(x),
即 ![]() =
= ![]() ,
,
解可得a=﹣1;
(2)解:由(1)可得a=﹣1,则f(x)= ![]() ,
,
则有f(1)=f(﹣1)=0,f(2)= ![]() ,
,
则集合E={y|y=f(x),x∈{﹣1,1,2}}={0, ![]() },
},
λ=(lg 2)2+lg 2lg 5+lg 5﹣ ![]() =lg2(lg2+lg5)+lg5﹣
=lg2(lg2+lg5)+lg5﹣ ![]() =lg2+lg5﹣
=lg2+lg5﹣ ![]() =
= ![]() ,
,
则有λ∈E;
(3)解:由(1)可得a=﹣1,则f(x)= ![]() =1﹣
=1﹣ ![]() ,则函数在(0,+∞)为增函数,
,则函数在(0,+∞)为增函数,
若当x∈[ ![]() ,
, ![]() ](m>0,n>0)时,函数f(x)的值域为[2﹣3m,2﹣3n],
](m>0,n>0)时,函数f(x)的值域为[2﹣3m,2﹣3n],
则有 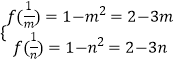 ,
,
解可得m= ![]() ,n=
,n= ![]() ,
,
又由 ![]() <
< ![]() 且m>0,n>0,则有0<n<m,
且m>0,n>0,则有0<n<m,
则m= ![]() ,n=
,n= ![]() .
.
【解析】(1)根据题意,由函数奇偶性的性质建立方程 ![]() =
= ![]() ,解可得a的值;(2)由(1)可得a的值,即可得函数的解析式,由此可得集合E,由对数的运算性质计算可得λ的值,分析可得答案;(3)由(1)可得函数的解析式,进而可以断函数的单调性,结合函数的值域建立方程关系进行求解即可.
,解可得a的值;(2)由(1)可得a的值,即可得函数的解析式,由此可得集合E,由对数的运算性质计算可得λ的值,分析可得答案;(3)由(1)可得函数的解析式,进而可以断函数的单调性,结合函数的值域建立方程关系进行求解即可.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+1(a∈R).
(1)若关于x的不等式f(x)≥0的解集为R,求实数a的取值范围;
(2)若关于x的不等式f(x)<0的解集是{x|b<x<2},求a,b的值;
(3)若关于x的不等式f(x)≤0的解集是 P,集合Q={x|0≤x≤1},若 P∩Q=,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元.甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1小时、2小时,加工一件乙产品所需工时分别为2小时、1小时,A、B两种设备每月有效使用台时数分别为400小时和500小时.如何安排生产可使月收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) 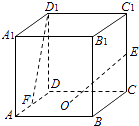
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数g(x)= ![]() +lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣
+lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx﹣ ![]() ﹣lnx(m∈R).
﹣lnx(m∈R).
(Ⅰ)求θ的值;
(Ⅱ)若f(x)﹣g(x)在[1,+∞)上为单调函数,求m的取值范围;
(Ⅲ)设h(x)= ![]() ,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
,若在[1,e]上至少存在一个x0 , 使得f(x0)﹣g(x0)>h(x0)成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,acosC+ ![]() asinC﹣b﹣c=0.
asinC﹣b﹣c=0.
(1)求角A;
(2)若a=2,△ABC的面积为 ![]() ,求b,c.
,求b,c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,点P是平面A1BC1内一动点,且满足|PD|+|PB1|=6,则点P的轨迹所形成的图形的面积是( ) 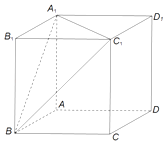
A.2π
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(t,t),点M是圆O1:x2+(y﹣1)2= ![]() 上的动点,点N是圆O2:(x﹣2)2+y2=
上的动点,点N是圆O2:(x﹣2)2+y2= ![]() 上的动点,则|PN|﹣|PM|的最大值是( )
上的动点,则|PN|﹣|PM|的最大值是( )
A.1
B.![]() ﹣2
﹣2
C.2+ ![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com