
【题目】若方程![]() 有实数根
有实数根![]() ,则称
,则称![]() 为函数
为函数![]() 的一个不动点.已知函数
的一个不动点.已知函数![]() (
(![]() ).
).
(1)若![]() ,求证:
,求证:![]() 有唯一不动点;
有唯一不动点;
(2)若![]() 有两个不动点,求实数a的取值范围.
有两个不动点,求实数a的取值范围.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)依题意,令![]() (
(![]() ),利用导数可知
),利用导数可知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,且
上单调递增,且![]() 时,
时,![]() 取的最小值0,由此即可得出结论;
取的最小值0,由此即可得出结论;
(2)先证明![]() ,则
,则![]() 有两个不动点等价于函数
有两个不动点等价于函数![]() 在
在![]() 上有两个不同的零点,求出
上有两个不同的零点,求出![]() 的导数,得到其单调性,得到函数的最小值
的导数,得到其单调性,得到函数的最小值![]() ,即可得到
,即可得到![]() 的取值范围,再证明
的取值范围,再证明![]() 时,
时,![]() 有两个零点;
有两个零点;
解:(1)证明:当![]() 时,由
时,由![]() 得
得![]() ,
,
令![]() (
(![]() ),
),
则![]() ,易知
,易知![]() 在
在![]() 上恒成立,
上恒成立,
故当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴方程![]() 有唯一实数根
有唯一实数根![]() ,故
,故![]() 有唯一不动点;
有唯一不动点;
(2)先证明![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,从而
,从而![]() ,因此
,因此![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,所以
,所以![]() ,即
,即![]() ,
,![]() 有两个不动点等价于函数
有两个不动点等价于函数![]() 在
在![]() 上有两个不同的零点,
上有两个不同的零点,
易知![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以有
,所以有![]() ,所以
,所以![]() ,即
,即![]() ,
,
下面说明![]() 时,
时,![]() 有两个零点,取
有两个零点,取![]() 有
有![]() ,故
,故![]() ,取
,取![]() ,且
,且![]() ,故
,故![]() ,又
,又![]() ,由零点存在性定理知
,由零点存在性定理知![]() 在
在![]() 存在唯一
存在唯一![]() ,使得
,使得![]() ,在
,在![]() 内存在
内存在![]() 使
使![]() ,综上有
,综上有![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】国家统计局统计了我国近10年(2009年2018年)的GDP(GDP是国民经济核算的核心指标,也是衡量一个国家或地区总体经济状况的重要指标)增速的情况,并绘制了下面的折线统计图.

根据该折线统计图,下面说法错误的是
A. 这10年中有3年的GDP增速在9.00%以上
B. 从2010年开始GDP的增速逐年下滑
C. 这10年GDP仍保持6.5%以上的中高速增长
D. 2013年—2018年GDP的增速相对于2009年—2012年,波动性较小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数![]() (其中
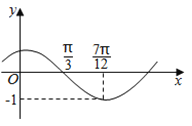
(其中![]() )的图象如图所示,为了得到
)的图象如图所示,为了得到![]() 的图象,则只要将
的图象,则只要将![]() 的图象上所有的点( )
的图象上所有的点( )
A.向左平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
B.向左平移![]() 个单位长度,纵坐标伸长到原来的3倍横坐标不变
个单位长度,纵坐标伸长到原来的3倍横坐标不变
C.向右平移![]() 个单位长度,纵坐标缩短到原来的
个单位长度,纵坐标缩短到原来的![]() ,横坐标不变
,横坐标不变
D.向右平移![]() 个单位长度,纵坐标伸长到原来的3倍,横坐标不变
个单位长度,纵坐标伸长到原来的3倍,横坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂加工的零件按箱出厂,每箱有10个零件,在出厂之前需要对每箱的零件作检验,人工检验方法如下:先从每箱的零件中随机抽取4个零件,若抽取的零件都是正品或都是次品,则停止检验;若抽取的零件至少有1个至多有3个次品,则对剩下的6个零件逐一检验.已知每个零件检验合格的概率为0.8,每个零件是否检验合格相互独立,且每个零件的人工检验费为2元.
(1)设1箱零件人工检验总费用为![]() 元,求
元,求![]() 的分布列;
的分布列;
(2)除了人工检验方法外还有机器检验方法,机器检验需要对每箱的每个零件作检验,每个零件的检验费为1.6元.现有1000箱零件需要检验,以检验总费用的数学期望为依据,在人工检验与机器检验中,应该选择哪一个?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,是否存在整数
时,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中.已知:数列
这三个条件中任选一个,补充在下面问题中.已知:数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() , .求:对大于1的自然数
, .求:对大于1的自然数![]() ,是否存在大于2的自然数
,是否存在大于2的自然数![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列.若存在,求
成等比数列.若存在,求![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某款电视机的寿命,研究人员对该款电视机进行了相应的测试,将得到的数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并统计如图所示:
,并统计如图所示:
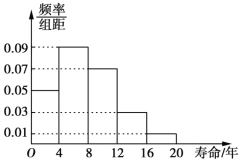
并对不同性别的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款电视机 | 不愿意购买该款电视机 | 总计 | |
男性 | 800 | 1000 | |
女性 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均寿命;
(2)根据表中数据,能否在犯错误的概率不超过0.001的前提下认为“是否愿意购买该款电视机”与“市民的性别”有关;
(3)以频率估计概率,若在该款电视机的生产线上随机抽取4台,记其中寿命不低于4年的电视机的台数为X,求X的分布列及数学期望.
参考公式及数据: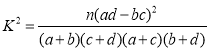 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com