解:(Ⅰ)直线AB、AC、BC的方程依次为
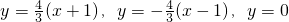
.点P(x,y)到AB、AC、BC的距离依次为

.依设,d
1d
2=d
32,得|16x
2-(3y-4)
2|=25y
2,即16x
2-(3y-4)
2+25y
2=0,或16x
2-(3y-4)
2-25y
2=0,化简得点P的轨迹方程为
圆S:2x
2+2y
2+3y-2=0与双曲线T:8x
2-17y
2+12y-8=0
(Ⅱ)由前知,点P的轨迹包含两部分
圆S:2x
2+2y
2+3y-2=0①
与双曲线T:8x
2-17y
2+12y-8=0②△ABC的内心D也是适合题设条件的点,由d
1=d
2=d
3,解得

,且知它在圆S上.直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为
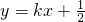
③
(i)当k=0时,L与圆S相切,有唯一的公共点D;此时,直线

平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点.
(ii)当k≠0时,L与圆S有两个不同的交点.这时,L与点P的轨迹恰有3个公共点只能有两种情况:
情况1:直线L经过点B或点C,此时L的斜率

,直线L的方程为x=±(2y-1).代入方程②得y(3y-4)=0,解得
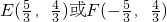
.表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F.
故当

时,L恰好与点P的轨迹有3个公共点.(11分)
情况2:直线L不经过点B和C(即

),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点.即方程组
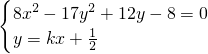
有且只有一组实数解,消去y并化简得
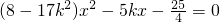
该方程有唯一实数解的充要条件是8-17k
2=0④
或

⑤
解方程④得
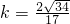
,解方程⑤得

.
综合得直线L的斜率k的取值范围
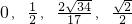
.(14分)
分析:(Ⅰ)直线AB、AC、BC的方程依次为
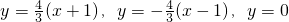
.点P(x,y)到AB、AC、BC的距离依次为

.由此能求出点P的轨迹方程.
(Ⅱ)点P的轨迹包含圆S:2x
2+2y
2+3y-2=0与双曲线T:8x
2-17y
2+12y-8=0.△ABC的内心D也是适合题设条件的点,由d
1=d
2=d
3,解得

.设L的方程为
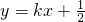
.再分情况讨论能够求出直线L的斜率k的取值范围.
点评:求题考查点的轨迹方程的求法和求L的斜率k的取值范围,解题时要认真审题,注意分类讨论思想的合理运用,利用圆锥曲线的性质恰当地进行等价转化.

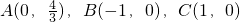 ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项.
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项.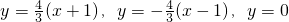 .点P(x,y)到AB、AC、BC的距离依次为
.点P(x,y)到AB、AC、BC的距离依次为 .依设,d1d2=d32,得|16x2-(3y-4)2|=25y2,即16x2-(3y-4)2+25y2=0,或16x2-(3y-4)2-25y2=0,化简得点P的轨迹方程为
.依设,d1d2=d32,得|16x2-(3y-4)2|=25y2,即16x2-(3y-4)2+25y2=0,或16x2-(3y-4)2-25y2=0,化简得点P的轨迹方程为 ,且知它在圆S上.直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为
,且知它在圆S上.直线L经过D,且与点P的轨迹有3个公共点,所以,L的斜率存在,设L的方程为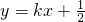 ③
③ 平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点.
平行于x轴,表明L与双曲线有不同于D的两个公共点,所以L恰好与点P的轨迹有3个公共点. ,直线L的方程为x=±(2y-1).代入方程②得y(3y-4)=0,解得
,直线L的方程为x=±(2y-1).代入方程②得y(3y-4)=0,解得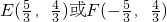 .表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F.
.表明直线BD与曲线T有2个交点B、E;直线CD与曲线T有2个交点C、F. 时,L恰好与点P的轨迹有3个公共点.(11分)
时,L恰好与点P的轨迹有3个公共点.(11分) ),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点.即方程组
),因为L与S有两个不同的交点,所以L与双曲线T有且只有一个公共点.即方程组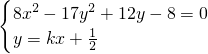 有且只有一组实数解,消去y并化简得
有且只有一组实数解,消去y并化简得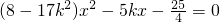
 ⑤
⑤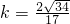 ,解方程⑤得
,解方程⑤得 .
.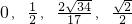 .(14分)
.(14分)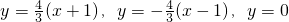 .点P(x,y)到AB、AC、BC的距离依次为
.点P(x,y)到AB、AC、BC的距离依次为 .由此能求出点P的轨迹方程.
.由此能求出点P的轨迹方程. .设L的方程为
.设L的方程为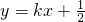 .再分情况讨论能够求出直线L的斜率k的取值范围.
.再分情况讨论能够求出直线L的斜率k的取值范围.

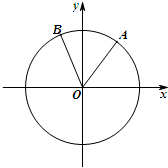 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.