
| A. | $[2-\frac{{2\sqrt{3}}}{3},2+\frac{{2\sqrt{3}}}{3}]$ | B. | $[1,2+\frac{{2\sqrt{3}}}{3}]$ | C. | $[2-\frac{{2\sqrt{3}}}{3},3]$ | D. | [1,3] |
分析 由函数f(x)是递增函数,且y=f(x-1)的图象关于点(1,0)对称,可得函数f(x)是奇函数,
再结合f(n-3)+f($\sqrt{4m{-m}^{2}-3}$)=0可得(n-3)+$\sqrt{4m{-m}^{2}-3}$=0,进而利用数形结合求出结果.
解答 解:f(x)是定义在R上的增函数,且函数y=f(x-1)的图象关于点(1,0)对称,
所以函数f(x)是奇函数;
又f(n-3)+f($\sqrt{4m{-m}^{2}-3}$)=0,
所以(n-3)+$\sqrt{4m{-m}^{2}-3}$=0,且4m-m2-3≥0;
即$\left\{\begin{array}{l}{{(m-2)}^{2}{+(n-3)}^{2}=1}\\{1≤m≤3}\\{2≤n≤3}\end{array}\right.$,
画出不等式组表示的图形,如图所示;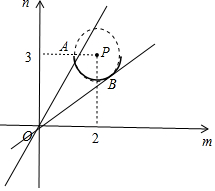
则实数m,n表示一段圆弧,
所以$\frac{n}{m}$表示圆弧上的点(m,n)与点(0,0)连线的斜率,
所以结合图象可得:$\frac{n}{m}$的最大值是直线OA的斜率,为$\frac{3-0}{1-0}$=3,
最小值是直线OB的斜率,不妨设为k,
则$\left\{\begin{array}{l}{n=km}\\{{(m-2)}^{2}{+(n-3)}^{2}=1}\end{array}\right.$,
消去n,得(m-2)2+(km-3)2=1,
整理得(k2+1)m2-(6k+4)m+12=0,
令△=(6k+4)2-4×12×(k2+1)=0,
化简得3k2-12k+8=0,
解得k=2±$\frac{2\sqrt{3}}{3}$,
应取k=2-$\frac{2\sqrt{3}}{3}$为最小值;
所以$\frac{n}{m}$的取值范围是:[2-$\frac{2\sqrt{3}}{3}$,3].
故选:C.
点评 本题考查了抽象函数的性质与应用问题,也考查了掌握知识与运用知识的能力,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | a<b<c | C. | c<b<a | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{n}$,$\frac{1}{m}$) | B. | ($\frac{1}{m}$,$\frac{1}{n}$) | C. | (-∞,$\frac{1}{n}$)∪($\frac{1}{m}$,+∞) | D. | (-∞,$\frac{1}{m}$)∪($\frac{1}{n}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥面ABCD,PA=BC=4,AD=2,AC=AB=3,AD∥BC,N是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,PA=BC=4,AD=2,AC=AB=3,AD∥BC,N是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=0.5x2,x∈N* | B. | y=2x,x∈N* | C. | y=2x-1,x∈N* | D. | y=2x-2,x∈N* |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com