
分析 根据三角函数的诱导公式进行化简即可.
解答 解:(1)原式=$\frac{sinα(-sin(90°-α))cotα}{cosαtan(90°+α)tan(-α)}$=$\frac{-sinαcosαcotα}{cosαcotαtanα}$=-cosα;
(2)原式=1+sinα•(-sinα)-2cos2α=1-sin2α-2cos2α=cos2α-2cos2α=-cos2α.
(3)$\frac{\sqrt{1-2sin100°cos280°}}{cos370°-\sqrt{1-co{s}^{2}170°}}$=$\frac{\sqrt{1-2sin100°cos280°}}{cos10°-sin170°}$=$\frac{(\;\;\;\;)}{(\;\;\;\;)}$$\frac{\sqrt{1+sin200°}}{cos10°-sin10°}=\frac{\sqrt{1-sin20°}}{cos10°-sin10°}$=$\frac{\sqrt{(cos10°-sin10°)^{2}}}{cos10°-sin10°}$
=$\frac{cos10°-sin10°}{cos10°-sin10°}$=1;
(4)$\frac{cos(α-π)•cot(5π-α)}{tan(2π-α)•sin(-2π-α)}$=$\frac{-cosα•(-cotα)}{-tanα•(-sinα)}$=$\frac{co{s}^{3}α}{si{n}^{3}α}$.
点评 本题主要考查三角函数值的化简,利用三角函数的诱导公式是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
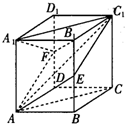 如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为6,点E、F分别是BB1、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
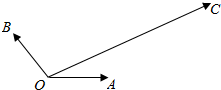 如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=2$\sqrt{3}$,用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$.
如图,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1,$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为120°,$\overrightarrow{OC}$与$\overrightarrow{OA}$的夹角为30°,|$\overrightarrow{OC}$|=2$\sqrt{3}$,用$\overrightarrow{OA}$、$\overrightarrow{OB}$表示$\overrightarrow{OC}$为$\overrightarrow{OC}$=4$\overrightarrow{OA}$+2$\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{4}{3}$) | B. | (-∞,0)∪($\frac{4}{3}$,+∞) | C. | (-∞,0]∪[$\frac{4}{3}$,+∞) | D. | [0,$\frac{2}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com