
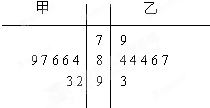
 如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.
如图是校园“十佳歌手”大奖赛上,七位评委为甲、乙两位选手打出的分数的茎叶图.

科目:高中数学 来源: 题型:
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
A、向左平移
| ||||
B、向右平移
| ||||
C、横坐标缩短到原来的
| ||||
D、横坐标缩短到原来的
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、方程f(x)=k(k∈R)有且仅有一个解 |
| B、函数f(x)的最大值为1 |
| C、函数f(x)是增函数 |
| D、函数f(x)的最小值为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某天甲、乙两同学约好在晚上8点到9点之间在某地会面,假定两人到达指定地点的时刻是等可能的且相互独立的,并约定先到者等待后到者时间是15分钟,之后就可以离去,问两人能够见面的概率有多大?
某天甲、乙两同学约好在晚上8点到9点之间在某地会面,假定两人到达指定地点的时刻是等可能的且相互独立的,并约定先到者等待后到者时间是15分钟,之后就可以离去,问两人能够见面的概率有多大?查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com