
【题目】如图,四棱锥![]() 的底面
的底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,点
,点![]() 为
为![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)推导出![]() 平面
平面![]() ,可得出
,可得出![]() ,再由
,再由![]() ,利用线面垂直的判定定理可得出
,利用线面垂直的判定定理可得出![]() 平面
平面![]() ,利用面面垂直的判定定理可证得结论成立;
,利用面面垂直的判定定理可证得结论成立;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,由
,由![]() 平面
平面![]() ,可得出直线
,可得出直线![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,计算出
,计算出![]() 、
、![]() ,推导出
,推导出![]() 平面
平面![]() ,计算出
,计算出![]() ,计算出点
,计算出点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,进而可得出直线
,进而可得出直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(1)证明:![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() ,
,
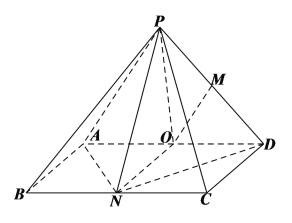
由(1)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() 即为直线
即为直线![]() 和平面
和平面![]() 所成的角,
所成的角,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 为
为![]() 中点,
中点,![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点,
中点,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
在矩形![]() 中,
中,![]() 且
且![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 点
点![]() 与点
与点![]() 到平面
到平面![]() 距离相等,设点
距离相等,设点![]() 到平面
到平面![]() 距离为
距离为![]() ,则
,则![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
则直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成面积为
的两焦点与短轴的一个端点的连线构成面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆E的标准方程;
(2)直线![]() 与椭圆交于点A、B,线段
与椭圆交于点A、B,线段![]() 的中点为M,射线MO与椭圆交于点P,点O为
的中点为M,射线MO与椭圆交于点P,点O为![]() 的重心,试问:
的重心,试问:![]() 的面积S是否为定值,若是,求出这个值;若不是,求S的取值范围.
的面积S是否为定值,若是,求出这个值;若不是,求S的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
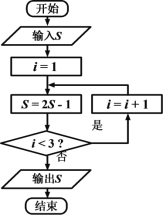
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年5月17日晚“2019年感动中国人物名单揭晓”,中国女排位列其中,在感动中国的舞台上,她们的一句“我们没赢够”,再次鼓舞中国人民中国之光——中国女排,一次次在逆境中绝地反击,赢得奥运冠军,“女排精神”也是我们当前处于“新冠”逆境中的高三学子们学习的榜样,前进的动力.一次比赛中,中国女排能够闯入决赛的概率为0.8,在闯入决赛条件下中国女排能够获胜的概率是0.9,则中国女排闯进决赛且获得冠军的概率是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北极冰融是近年来最引人注目的气候变化现象之一白色冰面融化变成颜色相对较暗的海冰,被称为“北极变暗”现象,21世纪以来,北极的气温变化是全球平均水平的2倍,被称为“北极放大”现象.如图为北极年平均海冰面积(![]() )与年平均
)与年平均![]()
![]() 浓度图.则下列说法正确的是( )
浓度图.则下列说法正确的是( )
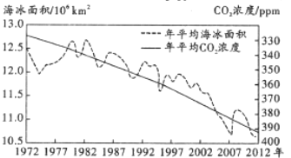
A.北极年海冰面积逐年减少
B.北极年海冰面积减少速度不断加快
C.北极年海冰面积与年平均二氧化碳浓度大体成负相关
D.北极年海冰面积与年平均二氧化碳浓度大体成正相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四边形![]() 是梯形(如图1),
是梯形(如图1),![]() ,
,![]() ,
,![]() ,
,![]() ,E为
,E为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点D到达点P的位置(如图2),且
折起,使点D到达点P的位置(如图2),且![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求点C到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com