
(本小题满分为14分)定义在(-1,1)上的函数![]() 满足:
满足:
①对任意![]() 都有
都有![]() ;
;
②![]() 在
在![]() 上是单调递增函数,
上是单调递增函数,![]() .
.
求![]() 的值;
的值;
证明![]() 为奇函数;
为奇函数;
解不等式![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
. (本小题满分14分)
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:

(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数条形图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源:江苏省镇江市09-10学年高二第二学期期末考试数学试题理科 题型:解答题
(本小题满分14分)
某校从参加高一年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段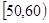 ,
,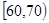 …
…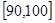 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题
(1)求出物理成绩低于50分的学生人数
(2)估计这次考试物理学科及格率(60分及以上为及格)
(3)从物理成绩不及格的学生中选两人,求他们成绩至少有一个不低于50分的概率.

查看答案和解析>>
科目:高中数学 来源:2010年广东省高一上学期期中考试数学卷 题型:解答题
(本小题满分为14分)定义在(-1,1)上的函数 满足:
满足:
①对任意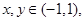 都有
都有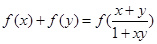 ;
;
② 在
在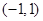 上是单调递增函数,
上是单调递增函数,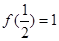 .
.
(1)求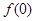 的值;
的值;
(2)证明 为奇函数;
为奇函数;
(3)解不等式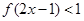 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(2010广东理数)20.(本小题满分为14分)
一条双曲线![]() 的左、右顶点分别为A1,A2,点
的左、右顶点分别为A1,A2,点![]() ,
,![]() 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。
(1)求直线A1P与A2Q交点的轨迹E的方程式;
(2)若过点H(0, h)(h>1)的两条直线l1和l2与轨迹E都只有一个交点,且![]() ,求h的值。
,求h的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com