
【题目】已知抛物线![]() ,过焦点
,过焦点![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() ,
,![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的准线上一点,且
的准线上一点,且![]() 的面积为4.
的面积为4.
(1)求抛物线![]() 的标准方程.
的标准方程.
(2)设![]() ,若点
,若点![]() 是抛物线
是抛物线![]() 上的任一动点,则是否存在垂直于
上的任一动点,则是否存在垂直于![]() 轴的定直线被以
轴的定直线被以![]() 为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
为直径的圆截得的弦长为定值?如果存在,求出该直线方程和弦长,如果不存在,说明理由.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°、距离A为10海里的C处,并测得渔船正沿方位角105°的方向,以9海里/时的速度向某小岛B靠拢,我海军舰艇立即以21海里/时的速度前去营救,恰在小岛B处追上渔船.
(1)试问舰艇应按照怎样的航向前进?
(2)求出舰艇靠近渔船所用的时间?
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率Q与日产量x(万件)之间满足关系,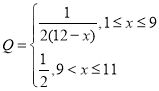 ,已知每生产1万件合格的产品盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量x(万件)的函数;
(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差图中残差点所在的水平带状区域越窄,则回归方程的预报精确度越高;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当变量
中,当变量![]() 每增加1个单位时,变量
每增加1个单位时,变量![]() 就增加2个单位
就增加2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强
之间的负相关很强
以上正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于![]() 的同学中任选
的同学中任选![]() 人,求选到的
人,求选到的![]() 人身高都在
人身高都在![]() 以下的概率
以下的概率
(Ⅱ)从该小组同学中任选![]() 人,求选到的
人,求选到的![]() 人的身高都在
人的身高都在![]() 以上且体重指标都在
以上且体重指标都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A是椭圆![]() 的左顶点,点P,Q在椭圆上且均在x轴上方.
的左顶点,点P,Q在椭圆上且均在x轴上方.
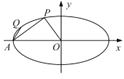
(1)若直线AP与OP垂直,求点P的坐标;
(2)若直线AP,AQ的斜率之积为![]() ,求直线PQ的斜率的取值范围.
,求直线PQ的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com