
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1 , ACC1A1均为正方形,AB=AC=1,∠BAC=90,点D是棱B1C1的中点. 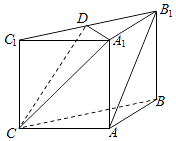
(1)求证:AB1∥平面A1DC;
(2)求证:A1D⊥平面BB1C1C.
【答案】
(1)证明:连结AC1交A1C于O点,连结OD,
∵四边形AA1C1C是正方形,∴O是AC1的中点,
又点D是棱B1C1的中点,
∴OD∥AB1,∵AB1平面A1DC,OD平面A1DC,
∴AB1∥平面A1DC

(2)证明:∵侧面ABB1A1,ACC1A1均为正方形,
∴A1A⊥A1C1,A1A⊥A1B1,又A1C1平面A1B1C1,A1B1平面A1B1C1,A1B1∩A1C1=A1,
∴A1A⊥平面A1B1C1,∵AA1∥CC1,
∴CC1⊥平面A1B1C1,∵A1D平面A1B1C1,
∴CC1⊥A1D.
又∵A1B1=AB=1,A1C1=AC=1,
∴A1B1=A1C1,∵D是B1C1的中点,
∴A1D⊥B1C1,
又CC1平面BCC1B1,B1C1平面BCC1B1,CC1∩B1C1=C1,
∴A1D⊥平面BCC1B1
【解析】(1)连结AC1交A1C于O点,连结OD,由中位线定理可得OD∥AB1 , 故而AB1∥平面A1DC;(2)由正方形的性质得出A1A⊥A1C1 , A1A⊥A1B1 , 故A1A⊥平面A1B1C1 , 于是CC1⊥平面A1B1C1 , 得出CC1⊥A1D.又三线合一得出A1D⊥B1C1 , 故而A1D⊥平面BB1C1C.
【考点精析】掌握直线与平面平行的判定和直线与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,点 ![]() 的极坐标是
的极坐标是![]() ,曲线
,曲线 ![]() 的极坐标方程为
的极坐标方程为![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为 ![]() 轴的正半轴建立平面直角坐标系,斜率为
轴的正半轴建立平面直角坐标系,斜率为 ![]() 的直线
的直线 ![]() 经过点
经过点![]() .
.
(1)写出直线 ![]() 的参数方程和曲线
的参数方程和曲线 ![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线 ![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,向量
,向量 ![]() ,函数f(x)=
,函数f(x)= ![]() .
.
(1)求函数f(x)的单调递增区间;
(2)将函数y=f(x)的图象上所有点向右平行移动 ![]() 个单位长度,得函数y=g(x)的图象,求函数y=g(x)在区间[0,π]上的值域.
个单位长度,得函数y=g(x)的图象,求函数y=g(x)在区间[0,π]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A(x1,y1),B(x2,y2)是过F的直线与抛物线的两个交点,求证:
(1)y1y2=-p2,![]() ;(2)
;(2)![]() 为定值;
为定值;
(3)以AB为直径的圆与抛物线的准线相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 在
在![]() 和
和![]() 处取得极值,且
处取得极值,且![]() ,曲线
,曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明关于![]() 的方程
的方程![]() 至多只有两个实数根(其中
至多只有两个实数根(其中![]() 是
是![]() 的导函数,
的导函数, ![]() 是自然对数的底数).
是自然对数的底数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com