


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省锦州市高一12月月考数学试卷(解析版) 题型:选择题
下列命题中正确命题的个数是( )
⑴ 三点确定一个平面; ⑵ 若点P不在平面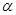 内,A、B、C三点都在平面
内,A、B、C三点都在平面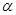 内,则P、A、B、C四点不在同一平面内; ⑶ 两两相交的三条直线在同一平面内; ⑷ 两组对边分别相等的四边形是平行四边形。
内,则P、A、B、C四点不在同一平面内; ⑶ 两两相交的三条直线在同一平面内; ⑷ 两组对边分别相等的四边形是平行四边形。
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2014届吉林油田高中高一第二学期期中考试数学试卷(解析版) 题型:填空题
下列命题中正确命题的序号是 .(把你认为正确的序号都填上)
①存在实数 ,使
,使 ;②若
;②若 是第一象限角,且
是第一象限角,且 ,则
,则 ;
;
③函数 是偶函数; ④函数
是偶函数; ④函数 的图象向左平移
的图象向左平移 个单位,得到函
个单位,得到函
数 的图象.
的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com