练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系，随机调查100名高一学生，得到列联表如下：由此得出的正确结论是( )

    选择物理

    不选择物理

    总计

    男

    35

    20

    55

    女

    15

    30

    45

    总计

    50

    50

    100

    附：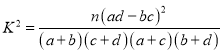

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    A.在犯错误的概率不超过0.01的前提下，认为“选择物理与性别有关”

    B.在犯错误的概率不超过0.01的前提下，认为“选择物理与性别无关”

    C.有的把握认为“选择物理与性别有关”

    D.有的把握认为“选择物理与性别无关”

    【答案】A

    【解析】

    根据公式计算出观测值，再根据临界值表可得结论.

    因为，

    根据临界值表可知，能在犯错误的概率不超过0.01的前提下，认为“选择物理与性别有关”.

    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，梯形ABCD所在的平面与等腰梯形ABEF所在的平面互相垂直，AB∥CD∥EF，AB⊥AD，CD＝DA＝AF＝FE＝2，AB＝4.

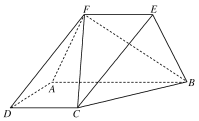
    (1)求证：DF∥平面BCE；

    (2)求二面角C—BF—A的正弦值；

    (3)线段CE上是否存在点G，使得AG⊥平面BCF？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直线()关于直线对称的直线为，直线，与椭圆分别交于点A，M和A，N，记直线的斜率为．

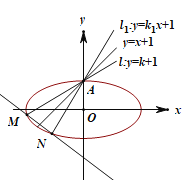
    （1）求的值；

    （2）当变化时，直线是否恒过定点？若恒过定点，求出该定点坐标；若不恒过定点，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有编号为1，2，3…n的n个学生，入座编号为1，2，3…n的n个座位，每个学生规定坐一个座位, 设学生所坐的座位号与该生的编号不同的学生人数为, 已知时, 共有6种坐法.

    （1）求的值；

    （2）求随机变量的概率分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正项数列的前项和为，且.

    （Ⅰ）试求数列的通项公式；

    （Ⅱ）设，求的前项和为.

    （Ⅲ）在（Ⅱ）的条件下，若对一切恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，记在点处的切线为.

    （1）当时，求证：函数的图像（除切点外）均为切线的下方；

    （2）当时，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝Asin（ωx+）（A＞0，ω＞0）的最小正周期为3π，则（　　）

    A. 函数f（x）的一个零点为

    B. 函数f（x）的图象关于直线x＝对称

    C. 函数f（x）图象上的所有点向左平移个单位长度后，所得的图象关于y轴对称

    D. 函数f（x）在（0，）上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】曲线C1的参数方程为 (θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.

    (1)求曲线C2和直线l的普通方程.

    (2)P为曲线C2上任意一点,求点P到直线l的距离的最值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

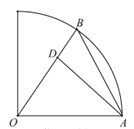
    【题目】某校在圆心角为直角，半径为的扇形区域内进行野外生存训练.如图所示，在相距的，两个位置分别为300,100名学生，在道路上设置集合地点，要求所有学生沿最短路径到点集合，记所有学生进行的总路程为.

    （1）设，写出关于的函数表达式；

    （2）当最小时，集合地点离点多远？

    查看答案和解析>>

    同步练习册答案