
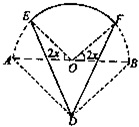
 如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,
如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,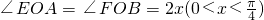 .若游客在每条路线上游览的“留恋度”均与相应的线段或弧的长度成正比,且“留恋度”与路线DE,DF的长度的比例系数为2,与路线EF的长度的比例系数为1,假定该风景区整体的“留恋度”y是游客游览所有路线“留恋度”的和.
.若游客在每条路线上游览的“留恋度”均与相应的线段或弧的长度成正比,且“留恋度”与路线DE,DF的长度的比例系数为2,与路线EF的长度的比例系数为1,假定该风景区整体的“留恋度”y是游客游览所有路线“留恋度”的和. =1,∠EOA=∠FOB=2x,所以弧AE等于弧BF的长等于2x,
=1,∠EOA=∠FOB=2x,所以弧AE等于弧BF的长等于2x,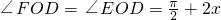 ,
, =
=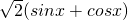 .
.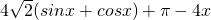 (0<x<
(0<x< );
);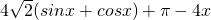 (0<x<
(0<x< ),
),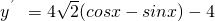 ,
,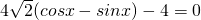 ,
,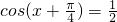 ,解得x=
,解得x= .
.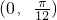 时,y′>0,所以此时y在
时,y′>0,所以此时y在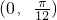 上单调递增,
上单调递增,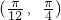 时,y′<0,所以此时y在
时,y′<0,所以此时y在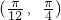 上单调递减,
上单调递减, 时,函数y有最大值,
时,函数y有最大值, 时,该风景区整体的“留恋度”最佳.
时,该风景区整体的“留恋度”最佳.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
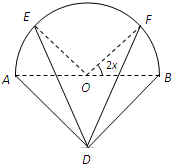 某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示.其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE,DF是两根支杆,其中AB=2米,∠EOA=∠FOB=2x(0<x<
某广告公司为2010年上海世博会设计了一种霓虹灯,样式如图中实线部分所示.其上部分是以AB为直径的半圆,点O为圆心,下部分是以AB为斜边的等腰直角三角形,DE,DF是两根支杆,其中AB=2米,∠EOA=∠FOB=2x(0<x<| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
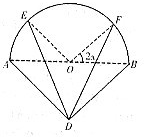 如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<
如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
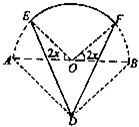 如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<
如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<| π | 4 |
查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市启东中学高考适应性考试数学试卷(解析版) 题型:解答题
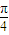 ).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.
).现在弧EF、线段DE与线段DF上装彩灯,在弧AE、弧BF、线段AD与线段BD上装节能灯.若每种灯的“心悦效果”均与相应的线段或弧的长度成正比,且彩灯的比例系数为2k,节能灯的比例系数为k(k>0),假定该霓虹灯整体的“心悦效果”y是所有灯“心悦效果”的和.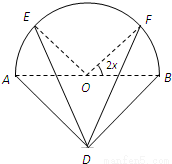
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com