
已知函数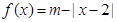 ,m∈R,且
,m∈R,且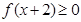 的解集为
的解集为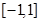 .
.
(1)求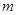 的值;
的值;
(2)若 +,且
+,且 ,求
,求 的最小值.
的最小值.
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
两个加油站A,B位于某城市东akm和bkm处(a<b),一卡车从该城市出发,由于某种原因,它需要往返A,B两加油站,问它行驶在什么情况下到两加油站的路程之和是一样的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com