
分析 双曲线16x2-9y2=144可化为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1,可得a=3,b=4,c=5,从而可求双曲线的实半轴长,虚半轴长,半焦距长,离心率,焦点坐标,顶点坐标,渐进线方程.
解答 解:(1)双曲线16x2-9y2=144可化为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1,
所以a=3,b=4,c=5,
所以,实半轴长为3,虚半轴长为4,半焦距长为5,离心率e=$\frac{c}{a}$=$\frac{5}{3}$;
(2)双曲线的焦点坐标(0,±5),顶点坐标(0,±3),渐进线方程y=±$\frac{4}{3}$x.
点评 本题考查双曲线的标准方程,考查双曲线的几何性质,确定双曲线的几何量是关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:解答题
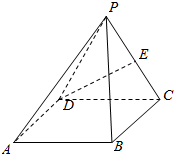 如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,侧面PDC是边长为a的正三角形,且平面PDC⊥底面ABCD,E为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{6}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
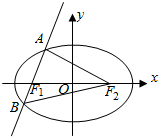 已知F1、F2为椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(a>b>0)的左、右两个焦点,斜率不为0的直线l过左焦点F1 且交椭圆C于A(x1,y1),B(x2,y2)两点,
已知F1、F2为椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(a>b>0)的左、右两个焦点,斜率不为0的直线l过左焦点F1 且交椭圆C于A(x1,y1),B(x2,y2)两点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
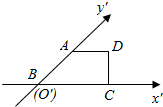 有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.
有一块多边形的菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图)∠ABC=45°,AB=$\sqrt{2}$,AD=1,DC⊥BC,则这块菜地的面积为$3\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
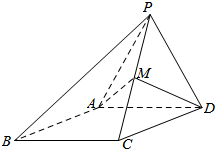 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面ABCD垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
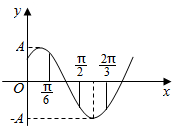 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的图象如图所示,若$f({\frac{π}{2}})=f({\frac{2π}{3}})=-f({\frac{π}{6}})$,则ω=2.
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的图象如图所示,若$f({\frac{π}{2}})=f({\frac{2π}{3}})=-f({\frac{π}{6}})$,则ω=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com