已知函数f(x)=ax2+(b-8)x-a-ab,当x∈(-∞,-3)∪(2,+∞)时,f(x)<0.当x∈(-3,2)时f(x)>0.
(Ⅰ)求f(x)在[0,1]内的值域;
(Ⅱ)若ax2+bx+c≤0的解集为R,求实数c的取值范围..
【答案】
分析:(Ⅰ)由题意得-3,2是方程ax
2+(b-8)x-a-ab=0的两根,故有
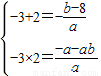
,且a<0,解得a和b,然后再根据函数单调性解出函数在在[0,1]内的值域即可;
(Ⅱ)在已知a和b的情况下,不等式ax
2+bx+c≤0的解集为R,列式
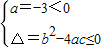
,可解出实数c的取值范围.
解答:解:(I)∵当x∈(-∞,-3)∪(2,+∞)时,f(x)<0.当x∈(-3,2)时f(x)>0
∴-3,2是方程ax2+(b-8)x-a-ab=0的两根,
∴可得
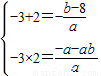
,所以 a=-3 b=5,
∴f(x)=-3x
2-3x+18=-3(x+

)
2+18.75
函数图象关于x=-0.5对称,且抛物线开口向下
∴在区间[0,1]上f(x)为减函数,所以函数的最大值为f(0)=18,最小值为f(1)=12
故f(x)在[0,1]内的值域为[12,18]
(II)由(I)知,不等式ax
2+bx+c≤0化为:-3x
2+5x+c≤0
因为二次函数y=:-3x
2+5x+c的图象开口向下,要使-3x
2+5x+c≤0的解集为R,只需
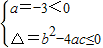
,
即 25+12c≤0⇒c≤
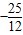
,
∴实数c的取值范围
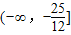
.
点评:本题考查二次函数的性质,一元二次不等式的解法,属于中档题.将一元二次不等式和一元二次方程以和二次函数相联系,采用数形结合的方法,是解决此种问题题的关键.
(I)采用一元二次方程根与系数关系,联解二元方程组,问题得解;
(II)结合函数图象,转化为抛物线所有的点在x轴下方或在x轴上的问题.

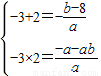 ,且a<0,解得a和b,然后再根据函数单调性解出函数在在[0,1]内的值域即可;
,且a<0,解得a和b,然后再根据函数单调性解出函数在在[0,1]内的值域即可;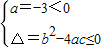 ,可解出实数c的取值范围.
,可解出实数c的取值范围.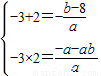 ,所以 a=-3 b=5,
,所以 a=-3 b=5, )2+18.75
)2+18.75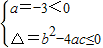 ,
,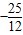 ,
,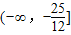 .
.
