
【题目】已知在直角梯形![]() 中,
中, ![]() ,
, ![]() ,将
,将![]() 沿
沿![]() 折起至
折起至![]() ,使二面角
,使二面角![]() 为直角.
为直角.
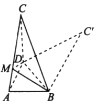
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若点![]() 满足
满足![]() ,
, ![]() ,当二面角
,当二面角![]() 为45°时,求
为45°时,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】为了让贫困地区的孩子们过一个温暖的冬天,某校阳光志愿者社团组织“这个冬天不再冷”冬衣募捐活动,共有50名志愿者参与.志愿者的工作内容有两项:①到各班做宣传,倡议同学们积极捐献冬衣;②整理、打包募捐上来的衣物.每位志愿者根据自身实际情况,只参与其中的某一项工作.相关统计数据如下表所示:

(1)如果用分层抽样的方法从参与两项工作的志愿者中抽取5人,再从这5人中选2人,那么“至少有1人是参与班级宣传的志愿者”的概率是多少?
(2)若参与班级宣传的志愿者中有12名男生,8名女生,从中选出2名志愿者,用![]() 表示所选志愿者中的女生人数,写出随机变量
表示所选志愿者中的女生人数,写出随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下五个关于圆锥曲线的命题中:
①平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹为![]() ;
;
②点P是抛物线![]() 上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则
上的动点,点P在y轴上的射影是M点A的坐标是A(3,6),则![]() 的最小值是6;
的最小值是6;
③平面内到两定点距离之比等于常数![]() 的点的轨迹是圆;
的点的轨迹是圆;
④若过点C(1,1)的直线![]() 交椭圆
交椭圆![]() 于不同的两点A,B,且C是AB的中点,则直线
于不同的两点A,B,且C是AB的中点,则直线![]() 的方程是
的方程是![]() .
.
⑤已知P为抛物线![]() 上一个动点,Q为圆
上一个动点,Q为圆![]() 上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是
上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是![]()
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为![]() ,
, ![]() ,
, ![]() (
(![]() ),设该同学三门课程都取得优秀成绩的概率为
),设该同学三门课程都取得优秀成绩的概率为![]() ,都未取得优秀成绩的概率为
,都未取得优秀成绩的概率为![]() ,且不同课程是否取得优秀成绩相互独立.
,且不同课程是否取得优秀成绩相互独立.
(1)求![]() ,
, ![]() ;
;
(2)设![]() 为该同学取得优秀成绩的课程门数,求
为该同学取得优秀成绩的课程门数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,将曲线![]() 的纵坐标不变,横坐标变为原来的2倍,得到曲线
的纵坐标不变,横坐标变为原来的2倍,得到曲线![]() ,过点
,过点![]() 作直线
作直线![]() ,交曲线
,交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年是内蒙古自治区成立70周年.某市旅游文化局为了庆祝内蒙古自治区成立70周年,举办了第十三届成吉思汗旅游文化周.为了了解该市关注“旅游文化周”居民的年龄段分布,随机抽取了![]() 名年龄在
名年龄在![]() 且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.

年龄 |
|
|
|
单人促销价格(单位:元) |
|
|
|
(Ⅰ)根据频率分布直方图,估计该市被抽取市民的年龄的平均数;
(Ⅱ)某旅行社针对“旅游文化周”开展不同年龄段的旅游促销活动,各年龄段的促销价位如表所示.已知该旅行社的运营成本为每人![]() 元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
(Ⅲ)若按照分层抽样的方法从年龄在![]() ,
, ![]() 的居民中抽取
的居民中抽取![]() 人进行旅游知识推广,并在知识推广后再抽取
人进行旅游知识推广,并在知识推广后再抽取![]() 人进行反馈,求进行反馈的居民中至少有
人进行反馈,求进行反馈的居民中至少有![]() 人的年龄在
人的年龄在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 在倾斜角为
在倾斜角为![]() 的直线
的直线![]() 上,以坐标原点
上,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的方程为
的方程为![]() .
.
(1)写出![]() 的参数方程及
的参数方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com