【题目】已知
.
（1）求函数
最值；
（2）若
，求证：
.
【答案】（1） 
取最大值
，无最小值；（2）详见解析.
【解析】
试题分析：（1）分析函数的导数，并且求函数的极值点，并且分析极值点两侧的单调性，求函数的最值；
（2）设
，根据（1）可知
，然后采用分析法的证明思路，转化为证明
，设
，
，根据函数的导数，可知函数是单调递增函数，所以
，得证.
试题解析：（1）对求导可得
，
令
得x=0.
当
时，
，函数单调递增；
当
时，
，函数单调递减，
当x=0时，取最大值，无最小值.
（2）不妨设，由（1）得
当
时，
，函数单调递增；
当
时，
，函数单调递减，
若
，则
，
欲证：
，只需证：
，
∵
函数在单调递减，
只需证：
，考虑到
，即证
，也即证
下证：
，
设
，
，
∴
，故g（x）在
上单调递增，
故时，g（x）<g（0）=0，即f（x）-f（-x）<0，∴
.
世纪百通期末金卷系列答案科目：高中数学 来源： 题型：
【题目】某城市要建成宜商、宜居的国际化现代新城，该城市的东城区、西城区分别引进8甲厂家，现对两个区域的16个厂家进行评估，综合得分情况如茎叶图所示.
（1）根据茎叶图判断哪个区域厂家的平均分较高；
（2）规定85分以上（含85分）为优秀厂家，若从该两个区域各选一个优秀厂家，求得分差距不超过5分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随机抽取某中学高一级学生的一次数学统测成绩得到一样本，其分组区间和频数是：
，2；
，7；
，10；
，x；[90，100]，2.其频率分布直方图受到破坏，可见部分如下图所示，据此解答如下问题.
（1）求样本的人数及x的值；
（2）估计样本的众数，并计算频率分布直方图中
的矩形的高；
（3）从成绩不低于80分的样本中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为
，求的数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了比较两种治疗失眠症的药(分别称为A药，B药)的疗效，随机地选取20位患者服用A药，20位患者服用B药，这40位患者在服用一段时间后，记录他们日平均增加的睡眠时间(单位：h)．试验的观测结果如下：
服用A药的20位患者日平均增加的睡眠时间：
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间：
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数，从计算结果看，哪种药的疗效更好？
(2)根据两组数据绘制茎叶图，从茎叶图看，哪种药的疗效更好？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
有如下性质：如果常数
，那么该函数在
上是减函数，在
上是增函数．
（1）已知
，利用上述性质，求函数
的单调区间和值域；
（2）对于（1）中的函数
和函数
，若对任意
，总存在
，使得
成立，求实数
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图（1）,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
AP=2,D是AP的中点,E,F,G分别是PC,PD,CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图（2）．
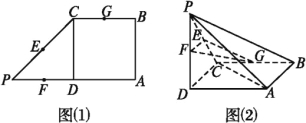
（1）求证:AP∥平面EFG;
（2）求三棱锥P-ABC的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
