
【题目】如图所示,已知⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P. (Ⅰ)求证:AD∥EC;
(Ⅱ)若AD是⊙O2的切线,且PA=6,PC=2,BD=9,求AD的长.
【答案】解:(Ⅰ)证明:连接AB, ∵AC是⊙O1的切线,
∴∠BAC=∠D,
又∵∠BAC=∠E,
∴∠D=∠E,
∴AD∥EC.
(Ⅱ)∵PA是⊙O1的切线,PD是⊙O1的割线,
∴PA2=PBPD,
∴62=PB(PB+9)
∴PB=3,
在⊙O2中由相交弦定理,得PAPC=BPPE,
∴PE=4,
∵AD是⊙O2的切线,DE是⊙O2的割线,
∴AD2=DBDE=9×16,
∴AD=12
【解析】(I)连接AB,根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D,又根据同弧所对的圆周角相等得到∠BAC=∠E,等量代换得到∠D=∠E,根据内错角相等得到两直线平行即可;(II)根据切割线定理得到PA2=PBPD,求出PB的长,然后再根据相交弦定理得PAPC=BPPE,求出PE,再根据切割线定理得AD2=DBDE=DB(PB+PE),代入求出即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在公比为2的等比数列{an}中,a2与a3的等差中项是9 ![]() .
.
(1)求a1的值;
(2)若函数y=|a1|sin( ![]() x+φ),|φ|<π,的一部分图象如图所示,M(﹣1,|a1|),N(3,﹣|a1|)为图象上的两点,设∠MPN=β,其中P与坐标原点O重合,0<β<π,求tan(φ﹣β)的值.
x+φ),|φ|<π,的一部分图象如图所示,M(﹣1,|a1|),N(3,﹣|a1|)为图象上的两点,设∠MPN=β,其中P与坐标原点O重合,0<β<π,求tan(φ﹣β)的值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校的学生文娱团队由理科组和文科组构成,具体数据如表所示:
组别 | 文科 | 理科 | ||
性别 | 男生 | 女生 | 男生 | 女生 |
人数 | 3 | 1 | 3 | 2 |
学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出,每选出一名男生,给其所在的组记1分;每选出一名女生,给其所在的组记2分,要求被选出的4人中文科组和理科组的学生都有.
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
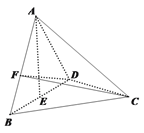
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有![]() 间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
间标准相同的客房,客房的定价将影响入住率.经调查分析,得出每间客房的定价与每天的入住率的大致关系如下表:
每间客房的定价 | 220元 | 200元 | 180元 | 160元 |
每天的入住率 |
|
|
|
|
对于每间客房,若有客住,则成本为80元;若空闲,则成本为40元.要使此宾馆每天的住房利润最高,则每间客房的定价大致应为( )
A. 220元 B. 200元 C. 180元 D. 160元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 在区间
在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,总存在
,总存在![]() 使
使![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 的值域为区间
的值域为区间![]() ,是否存在常数
,是否存在常数![]() ,使区间
,使区间![]() 的长度为
的长度为![]() ?若存在,求出
?若存在,求出![]() 的值,若不存在,请说明理由.(柱:区间
的值,若不存在,请说明理由.(柱:区间![]() 的长度为
的长度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2+y2≤4确定的平面区域为U,|x|+|y|≤1确定的平面区域为V.
(1)定义横、纵坐标为整数的点为“整点”,在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(2)在区域U内任取3个点,记这3个点在区域V的个数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com