关于x的不等式x2-(2a+1)x+a2+a-2≥0和x2-(a2+a)x+a3<0的解集分别为A、B,若A∩B=∅,求实数a的取值范围.
解:∵x
2-(2a+1)x+a
2+a-2≥0,∴(x-a-2)(x-a+1)≥0
∵a-1<a+2,∴A=(-∞,a-1]∪[a+2,+∞)(1分)
∵x
2-(a
2+a)x+a
3<0,∴(x-a)(x-a
2)<0
∴
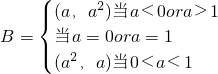
(2分)
∴当a<0ora>1时,∵a>a-1,∴
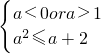
(2分)
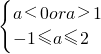
?-1≤a<0or1<a≤2(1分)
∴当0<a<1时,∵a<a+2,∴
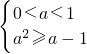
(1分)

?0<a<(11分)
∴当a=0ora=1时,∵B=∅∴A∩B=∅,∴a=0ora=(11分)
综上:-1≤a≤2(1分)
分析:先求出集合A,讨论a的大小求出集合B,然后根据A∩B=∅,分别建立不等式关系,解之即可求出实数a的取值范围.
点评:本题主要考查了一元二次不等式的解法,同时考查了分类讨论的数学思想,属于中档题.

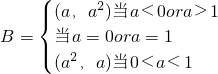 (2分)
(2分)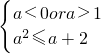 (2分)
(2分)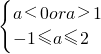 ?-1≤a<0or1<a≤2(1分)
?-1≤a<0or1<a≤2(1分)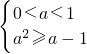 (1分)
(1分) ?0<a<(11分)
?0<a<(11分)

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案